算法思想 - 动态规划算法

1. 算法认识

1.1 什么是动态规划

动态规划（Dynamic Programming, DP） 是一种将原问题分解为若干个子问题，再将每个子问题的解进行记录或保存，以避免重复计算，从而获得高效求解的方法。在面临需要多次用到相同子问题结果的场景下，动态规划通常能够大大减少计算量。

与分治法（Divide and Conquer）类似，动态规划也通过分解来解决问题。然而，分治法 假定子问题之间是独立的，而 动态规划 适用于那些子问题之间存在重叠的情况。如果强行使用分治法，就会产生大量重复计算；而使用动态规划，可以将已经求解过的子问题结果保存起来，避免再次计算。

1.2 动态规划应用场景

动态规划主要用于求解具有最优性质的问题：有很多可行解，而我们需要找一个“最优解”。或求解“方案数”，即问“在满足某种条件下，有多少种不同的方式可以实现”。

常见的动态规划问题包括：

• 背包问题（0-1 背包、完全背包）
• 最长公共子序列（LCS）、最长上升子序列（LIS）
• 路径问题（如最短路径、最小路径和）
• 斐波那契数列（Fibonacci）
• 不同路径计数 等。

1.3 为什么需要动态规划

当一个问题通过“自顶向下”的递归或分治法来解决时，如果存在子问题重叠，同一个子问题会被多次计算，浪费大量时间。而动态规划通过“自底向上”（或记忆化“自顶向下”）的方式，将每个子问题的结果在第一次求解后存入表格，在后续需要该子问题结果时直接查表即可，省去了重复计算的开销。

简而言之：

• 分治法：适合子问题互不重复时；
• 动态规划：适合子问题有大量重叠时。

2. 动态规划的性质

2.1 子问题重叠

当使用递归法自顶向下求解时，会产生大量重复的子问题。例如，斐波那契数列 F(n) 的递归定义：

F(n) = F(n-1) + F(n-2)

求 F(5) 时，会递归产生 F(4), F(3), F(2) 等子问题，而 F(4) 又会产生 F(3), F(2), F(1) 等子问题，许多子问题（如 F(3), F(2)) 会被重复计算。

动态规划在第一次计算 F(3) 或 F(2) 时，就会把它们存储下来。以后再需要 F(3) 或 F(2) 的值时，就可以直接从存储位置取出，而无需再次递归计算。

2.2 状态转移方程

动态规划的核心在于找到正确的状态转移方程。 状态转移方程类似递归公式，用来表示当前状态的值和子问题之间的关系。

例如，斐波那契的状态转移方程可以这样写：

// 使用dp数组来存储结果
// dp[i] 表示斐波那契数列中第 i 个值
dp[i] = dp[i - 1] + dp[i - 2];

一旦定义好 dp[i] 的含义，并找到如何由子问题得到 dp[i]，就可以使用循环的方式，从底部往上填表。

示例：

• dp[i] = dp[i-1] + dp[i-2] （斐波那契）
• dp[i][j] = dp[i-1][j] + dp[i][j-1] （网格路径，每次只能往右或往下）
• 以及背包问题、最长公共子序列问题等，其状态转移方程会更复杂。

2.3 最优子结构

如果一个问题的最优解包含了其子问题的最优解（即“子问题的解一定也是最优解的一部分”），则认为该问题具有最优子结构。

示例：

• 背包问题：如果选择放入物品 i，那么背包剩余容量的最优解也一定是其子问题的最优解。
• 考试最高总成绩：语文、数学、英语都要分别考到最高分；要考到最高分，就要求各题型（选择题、填空题等）也分别做对，说明原问题的最优解由各子问题的最优解组成。

2.4 无后效性

动态规划要求，一旦当前阶段的状态已经确定，就不受后续阶段决策的影响；也就是 某一阶段的决策只依赖于之前做出的决策，与之后的决策无关。

示例：

• A -> B -> C 三个决策阶段
• 一旦确定了决策 A，后面的决策 B, C 并不会影响到已经做出的 A；而 B 会影响 C，但不影响已经过去的 A。

2.5 自底向上

在实现动态规划时，通常采用自底向上的方式来填表：

• 先计算最小规模子问题（如 dp[0] 或 dp[1]）
• 再根据状态转移方程一步步往上求，最终得到 dp[n]（或 dp[m][n]）
• 这种方式避免了大量递归，也比较容易理解和实现。

与此对应，还有一种记忆化搜索（Memoization）的实现方式，属于“自顶向下”式的动态规划：

• 先从最外层问题 F(n) 开始递归
• 当遇到子问题时，如果没有被计算过则计算并缓存结果；有则直接用缓存
• 最终也能达到与自底向上同样的效果。

2.6 初始条件

由于动态规划是自底向上，需要先知道最小规模子问题（或基础情况）的结果，然后才能逐步推出更大规模的结果。例如：

dp[0] = 0;
dp[1] = 1;
dp[n] = dp[n-1] + dp[n-2];

只要明确了初始条件，就能用状态转移方程逐步算到 dp[n]。

---

3. 动态规划的解题步骤

第一步：定义状态（dp 数组或 dp 表）

含义：我要用一个数组（或多维表格）来存储“子问题”的答案。 做法：

1. 想一想：如果我想知道“前 i 个元素（或前 i 阶楼梯、或前 i 个重量）”的结果，该怎么表示？
2. 通常会设计一个 dp[i]（一维）或 dp[i][j]（二维），让它记录你所关心的“最优值”或“总方法数”或“是否可行”等信息。

口决：“我想知道前 i 个的解，那就定义 dp[i] = …”

在很多动态规划（DP）的问题里，你会看到 dp 数组被定义为 int[] dp = new int[n + 1];，而不是 new int[n];。原因通常有以下几点：

1. 下标直接对应“第 i 个”
   • 如果你定义 dp[i] 表示“第 i 项”的答案（例如第 i 级台阶、前 i 个元素、等等），那就需要让数组下标能直接用 i 这个数字来访问。
   • 在 Java 中，数组是 0 开始的，索引范围是 [0, n-1]。如果你想使用 i 作为索引，而且 i 可能取值到 n，就需要一个长度为 n + 1 的数组，这样 dp[n] 才不会越界。
2. 需要存储 dp[0] 的初始状态
   • 在许多动态规划的题目中，dp[0] 可能也有其含义，比如：
     • “台阶数为 0 时的走法有 1 种（站在原地）”；
     • “没有物品时背包的最大价值是 0”；
     • “空字符串和某字符串的编辑距离为该字符串长度”，等等。
   • 这时，如果你的主要目标是 dp[n]，那在代码里就需要 dp[0] 也能访问，所以干脆开到 n+1。
3. 可读性更好，避免额外的偏移量
   • 如果你只开 n 长度的数组，那往往要用 dp[i-1] 来表示“第 i 项”，这会让索引变得有些混淆。
   • 而用 n+1 大小的数组时， dp[i] 就对应真正的“第 i 项”，可读性更强。

第二步：确定状态转移方程

含义：我怎么用前面已经算好的 dp[] 来得到当前 dp[i]？ 做法：

1. 问自己：“我算 dp[i] 的时候，能不能用 dp[i-1]、dp[i-2] 等更小指标的答案，来组合或比较？”
2. 常见的形式有：
   • dp[i] = dp[i-1] + dp[i-2]（比如斐波那契、爬楼梯）；
   • dp[i] = max(dp[i-1], dp[i-2] + something)（比如背包问题、打家劫舍）；
   • 甚至 dp[i][j] = max(dp[i-1][j], dp[i-1][j - weight] + value)（二维背包）。

口决：“我当前的最佳答案 = 以前某几个已知的答案做对比/相加/取最大最小”。

第三步：设置初始条件

含义：最小规模或特殊边界时，我们的答案是多少？ 做法：

1. 如果题目里已经给出最小的值（例如 dp[0] = 1、dp[1] = 1），就直接写上。
2. 如果题目没给，但逻辑能推出（如没有物品时背包价值=0，或者台阶数=0时走法=1），也要写在代码里。

口决：“我先把最小规模的答案填好，为后续计算铺路”。

第四步：计算顺序（自底向上）

含义：按照从小到大的顺序，依次填 dp 数组。 做法：

1. 先算 dp[0]、dp[1]，再算 dp[2]，直到 dp[n]。
2. 如果是二维 dp 表，就要把每一行或每一列先后顺序想清楚，一般是从 i=1 到 n，内层从 j=1 到 W 这样。

口决：“先小后大，把所有 dp[i] 都算出来，最后 dp[n] 就是答案”。

第五步：返回结果

含义：我们的最终目标往往就存在 dp[n] 或 dp[n][m] 里。 做法：

1. 大多数情况下，一维数组的答案就是 dp[n]；二维数组就是 dp[n][W]（背包问题为例）。
2. 如果问题需要路径或具体方案，有时还要用额外的方式做“回溯”或记录。

口决：“最后一步别忘了取 dp[n] 作为答案！”

---

4. 小试牛刀

动态规划（Dynamic Programming, DP）遵循一套固定的流程：递归的暴力解法 → 带备忘录的递归解法 → 非递归的动态规划解法。这个过程是层层递进地解决问题的方式，如果没有前面的铺垫，直接看最终的非递归动态规划解法，可能会难以理解其原理和优势。

4.1 斐波那契数列

斐波那契数列是动态规划中最经典的例子之一，适合用来演示从递归到动态规划的转变过程。

1-1 斐波那契数列定义

斐波那契数列的定义如下：

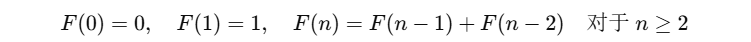
这意味着每一项都是前两项的和，例如：

• F(2)=F(1)+F(0)=1+0=1
• F(3)=F(2)+F(1)=1+1=2
• F(4)=F(3)+F(2)=2+1=3
• 以此类推。

1-2 暴力递归算法

最直观的方法是使用递归来直接实现斐波那契数列的定义。然而，这种方法存在大量的重复计算，导致时间复杂度呈指数级增长。

public class FibonacciRecursive {
    /**
     * 使用暴力递归法计算斐波那契数列第 n 项
     * 时间复杂度：O(2^n)
     * @param n 斐波那契数列的项数
     * @return 第 n 项的斐波那契数
     */
    public int fib(int n) {
        // 基本情况：F(0) = 0, F(1) = 1
        if (n == 0) return 0;
        if (n == 1) return 1;
        // 递归计算 F(n-1) + F(n-2)
        return fib(n - 1) + fib(n - 2);
    }

    public static void main(String[] args) {
        FibonacciRecursive solver = new FibonacciRecursive();
        int n = 20;
        System.out.println("Fibonacci(" + n + ") = " + solver.fib(n));
    }
}

问题分析：

• 递归过程：
  • 要计算 fib(n)，需要先计算 fib(n-1) 和 fib(n-2)。
  • fib(n-1) 又需要计算 fib(n-2) 和 fib(n-3)，如此反复，导致大量重复计算。
• 重复计算：
  • 许多子问题（如 fib(n-2)）会被多次计算，极大地增加了计算量。
• 时间复杂度：
  • 总时间复杂度为 O(2^n)，因为每个问题都分解成两个子问题，呈指数级增长。
• 空间复杂度：
  • 递归调用会使用栈空间，空间复杂度为 O(n)。

示例输出：

Fibonacci(20) = 6765

1-3 带备忘录的递归解法（记忆化递归）

为了避免重复计算，我们可以使用备忘录（Memoization）来存储已经计算过的子问题的结果。这样，在需要计算某个子问题时，先检查备忘录中是否已有结果，有则直接返回，避免再次递归计算。

import java.util.Arrays;

public class FibonacciMemoization {
    /**
     * 使用带备忘录的递归法计算斐波那契数列第 n 项
     * 时间复杂度：O(n)
     * 空间复杂度：O(n)
     * @param n 斐波那契数列的项数
     * @return 第 n 项的斐波那契数
     */
    public int fib(int n) {
        // 特殊情况处理
        if (n < 0) return -1; // 无效输入
        if (n == 0) return 0;
        if (n == 1) return 1;

        // 创建备忘录数组，初始化为 -1 表示未计算
        int[] memo = new int[n + 1];
        Arrays.fill(memo, -1);
        memo[0] = 0;
        memo[1] = 1;

        // 开始递归计算
        return fibMemo(n, memo);
    }

    /**
     * 递归辅助函数，使用备忘录存储已计算的结果
     * @param n 当前计算的项数
     * @param memo 备忘录数组
     * @return 第 n 项的斐波那契数
     */
    private int fibMemo(int n, int[] memo) {
        // 如果已经计算过，直接返回备忘录中的结果
        if (memo[n] != -1) {
            return memo[n];
        }

        // 递归计算 F(n-1) 和 F(n-2)，并存储在备忘录中
        memo[n] = fibMemo(n - 1, memo) + fibMemo(n - 2, memo);
        return memo[n];
    }

    public static void main(String[] args) {
        FibonacciMemoization solver = new FibonacciMemoization();
        int n = 20;
        System.out.println("Fibonacci(" + n + ") = " + solver.fib(n));
    }
}

代码说明：

1. 备忘录初始化：
   • 创建一个长度为 n+1 的数组 memo，并将所有元素初始化为 -1，表示尚未计算。
   • 设置 memo[0] = 0 和 memo[1] = 1，因为 F(0) 和 F(1) 的值已知。
2. 递归计算：
   • 在 fibMemo 方法中，首先检查 memo[n] 是否已计算过。
   • 如果已计算，直接返回 memo[n]。
   • 否则，递归计算 fibMemo(n-1, memo) 和 fibMemo(n-2, memo)，并将结果存储在 memo[n] 中。
3. 时间与空间复杂度：
   • 时间复杂度：O(n)，每个子问题只计算一次。
   • 空间复杂度：O(n)，用于存储备忘录和递归调用栈。

优化效果

• 带「备忘录」的递归算法，通过将一棵存在大量冗余的递归树通过「剪枝」，改造成一幅不存在冗余的递归图，极大减少了子问题（即递归图中节点）的个数。子问题的个数由原来的 O(2^n) 降低到 O(n)，所以该算法的时间复杂度是 O(n)。比起暴力算法，效率大幅度提升很多。
• 至此，带备忘录的递归解法的效率已经和动态规划一样了。实际上，这种解法和动态规划的思想已经差不多了，只不过这种方法叫做「自顶向下」，动态规划叫做「自底向上」，这也是为什么动态规划一般都脱离了递归，而是由循环迭代完成计算。

1-4 动态规划（自底向上）

有了「备忘录」的启发，我们可以将这个「备忘录」独立出来成为一张表，称为 dp，并在这张表上完成「自底向上」的推算。这种方法避免了递归带来的函数调用开销，并且更加直观易懂。

public class FibonacciDP {
    /**
     * 使用动态规划（自底向上）计算斐波那契数列第 n 项
     * 时间复杂度：O(n)
     * 空间复杂度：O(n)
     * @param n 斐波那契数列的项数
     * @return 第 n 项的斐波那契数
     */
    public int fib(int n) {
        // 特殊情况处理
        if (n < 0) return -1; // 无效输入
        if (n == 0) return 0;
        if (n == 1) return 1;

        // 创建 dp 数组，dp[i] 表示 F(i)
        int[] dp = new int[n + 1];
        dp[0] = 0; // F(0) = 0
        dp[1] = 1; // F(1) = 1

        // 逐步填充 dp 数组
        for (int i = 2; i <= n; i++) {
            // 状态转移方程：F(i) = F(i-1) + F(i-2)
            dp[i] = dp[i - 1] + dp[i - 2];
        }

        // 返回第 n 项的斐波那契数
        return dp[n];
    }

    public static void main(String[] args) {
        FibonacciDP solver = new FibonacciDP();
        int n = 20;
        System.out.println("Fibonacci(" + n + ") = " + solver.fib(n));
    }
}

代码说明：

1. dp数组定义：
   • dp[i] 表示第 i 项的斐波那契数。
2. 初始化：
   • dp[0] = 0，dp[1] = 1，因为 F(0) 和 F(1) 的值已知。
3. 填表过程：
   • 从 i = 2 到 i = n，依次计算 dp[i] = dp[i-1] + dp[i-2]。
   • 这一步根据状态转移方程，逐步构建更大规模的子问题解。
4. 返回结果：
   • 返回 dp[n]，即第 n 项的斐波那契数。
5. 时间与空间复杂度：
   • 时间复杂度：O(n)，只需一次遍历。
   • 空间复杂度：O(n)，用于存储 dp 数组。

示例输出：

Fibonacci(20) = 6765

dp[i] = dp[i - 1] + dp[i - 2]; 就是 状态转移方程，它是解决问题的核心。我们也很容易发现，其实状态转移方程直接代表着暴力解法。

动态规划问题最困难的就是写出状态转移方程。

1-5 动态规划优化（空间优化）

根据斐波那契数列的状态转移方程，当前状态只和之前的两个状态有关，其实并不需要那么长的一个 dp 数组来存储所有的状态，只需使用两个变量来保存前两项的值即可，从而将空间复杂度优化为 O(1)。

public class FibonacciOptimizedDP {
    /**
     * 使用动态规划优化（空间优化）计算斐波那契数列第 n 项
     * 时间复杂度：O(n)
     * 空间复杂度：O(1)
     * @param n 斐波那契数列的项数
     * @return 第 n 项的斐波那契数
     */
    public int fib(int n) {
        // 特殊情况处理
        if (n < 0) return -1; // 无效输入
        if (n == 0) return 0;
        if (n == 1) return 1;

        // 初始化前两项
        int prev = 0; // F(0)
        int curr = 1; // F(1)

        // 逐步计算
        for (int i = 2; i <= n; i++) {
            int sum = prev + curr; // F(i) = F(i-1) + F(i-2)
            prev = curr;           // 更新 F(i-2) 为 F(i-1)
            curr = sum;            // 更新 F(i-1) 为 F(i)
        }

        // 返回第 n 项的斐波那契数
        return curr;
    }

    public static void main(String[] args) {
        FibonacciOptimizedDP solver = new FibonacciOptimizedDP();
        int n = 20;
        System.out.println("Fibonacci(" + n + ") = " + solver.fib(n));
    }
}

代码说明：

1. 变量定义：
   • prev 表示 F(i-2)。
   • curr 表示 F(i-1)。
2. 计算过程：
   • 对于每个 i从 2 到 n：
     • 计算 sum = prev + curr，即 F(i)。
     • 更新 prev = curr，即 F(i-1) 变为新的 F(i-2)。
     • 更新 curr = sum，即 F(i) 变为新的 F(i-1)。
3. 返回结果：
   • 返回 curr，即第 n 项的斐波那契数。
4. 时间与空间复杂度：
   • 时间复杂度：O(n)，只需一次遍历。
   • 空间复杂度：O(1)，只使用了常数个变量。

示例输出：

Fibonacci(20) = 6765

这种优化方法充分利用了状态转移方程的特性，只保留了与当前状态相关的前两项，显著降低了空间复杂度。

4.2 硬币凑钱

问题描述：

给定 k 种不同面额的硬币，面额分别为 c1, c2, ..., ck，以及一个总金额 n，要求你编写一个函数来计算凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。

示例：

• 示例 1：
  • 输入：coins = [1, 2, 5], amount = 11
  • 输出：3
  • 解释：11 = 5 + 5 + 1
• 示例 2：
  • 输入：coins = [2], amount = 3
  • 输出：-1
  • 解释：无法凑成金额3
• 示例 3：
  • 输入：coins = [1, 3, 4], amount = 6
  • 输出：2
  • 解释：6 = 3 + 3

2-1 暴力递归算法

首先，我们可以用递归来解决这个问题。然而，暴力递归方法会导致大量的重复计算，时间复杂度非常高。

public class CoinChangeRecursive {
    /**
     * 使用暴力递归法计算凑成总金额所需的最少硬币数
     * 时间复杂度：O(k^n)，其中 k 是硬币种类数，n 是总金额
     * @param coins 不同面额的硬币数组
     * @param amount 总金额
     * @return 最少的硬币数，如果无法凑成，返回 -1
     */
    public int coinChange(int[] coins, int amount) {
        // 如果金额为0，则不需要任何硬币
        if (amount == 0) return 0;

        int ans = Integer.MAX_VALUE; // 初始化答案为一个很大的数

        // 遍历每个硬币，尝试选择它
        for (int coin : coins) {
            // 如果当前硬币面额大于金额，则跳过
            if (amount - coin < 0) continue;

            // 递归计算凑成剩余金额所需的硬币数
            int subProb = coinChange(coins, amount - coin);

            // 如果无法凑成剩余金额，跳过
            if (subProb == -1) continue;

            // 更新答案
            ans = Math.min(ans, subProb + 1);
        }

        // 如果 ans 仍为初始值，说明无法凑成目标金额
        return (ans == Integer.MAX_VALUE) ? -1 : ans;
    }

    public static void main(String[] args) {
        CoinChangeRecursive solver = new CoinChangeRecursive();
        int[] coins1 = {1, 2, 5};
        int amount1 = 11;
        System.out.println("最少硬币数（示例1）：" + solver.coinChange(coins1, amount1)); // 输出3

        int[] coins2 = {2};
        int amount2 = 3;
        System.out.println("最少硬币数（示例2）：" + solver.coinChange(coins2, amount2)); // 输出-1

        int[] coins3 = {1, 3, 4};
        int amount3 = 6;
        System.out.println("最少硬币数（示例3）：" + solver.coinChange(coins3, amount3)); // 输出2
    }
}

问题分析：

• 递归过程：
  • 要计算 coinChange(coins, amount)，需要尝试每种硬币，并递归计算凑成 amount - coin 的最少硬币数。
  • 例如，要计算 coinChange(coins, 11)，需要计算 coinChange(coins, 10)、coinChange(coins, 9) 和 coinChange(coins, 6)。
• 重复计算：
  • 许多子问题（如 coinChange(coins, 1)）会被多次计算，极大地增加了计算量。
• 时间复杂度：
  • 总时间复杂度为 O(k^n)，其中 k 是硬币种类数，n 是总金额。这是因为每个金额可能会递归调用 k 次，每次调用再递归调用 k 次，呈指数级增长。
• 空间复杂度：
  • 递归调用栈的深度为 O(n)，因此空间复杂度为 O(n)。

示例输出：

最少硬币数（示例1）：3
最少硬币数（示例2）：-1
最少硬币数（示例3）：2

2-2 带备忘录的递归解法（记忆化递归）

既然暴力递归算法存在效率低下的问题，主要原因是大量的重复计算，我们可以通过备忘录（Memoization）来优化这一点。每次计算一个子问题的结果后，先将其存储在备忘录中；下次遇到相同的子问题时，直接从备忘录中取出结果，而不再进行重复计算。

import java.util.Arrays;

public class CoinChangeMemoization {
    /**
     * 使用带备忘录的递归法计算凑成总金额所需的最少硬币数
     * 时间复杂度：O(k*n)，其中 k 是硬币种类数，n 是总金额
     * 空间复杂度：O(n)
     * @param coins 不同面额的硬币数组
     * @param amount 总金额
     * @return 最少的硬币数，如果无法凑成，返回 -1
     */
    public int coinChange(int[] coins, int amount) {
        // 备忘录数组，用于存储已经计算过的结果
        // 初始化为 -2，表示尚未计算
        int[] memo = new int[amount + 1];
        Arrays.fill(memo, -2);
        // 凑成0元需要0个硬币
        memo[0] = 0;
        // 开始递归计算
        return helper(coins, amount, memo);
    }

    /**
     * 递归辅助函数，使用备忘录存储已计算的结果
     * @param coins 硬币面额数组
     * @param amount 当前需要凑成的金额
     * @param memo 备忘录数组
     * @return 凑成当前金额所需的最少硬币数，如果无法凑成，返回 -1
     */
    private int helper(int[] coins, int amount, int[] memo) {
        // 如果金额为0，返回0
        if (amount == 0) return 0;

        // 如果已经计算过，直接返回备忘录中的结果
        if (memo[amount] != -2) {
            return memo[amount];
        }

        int ans = Integer.MAX_VALUE; // 初始化答案为一个很大的数

        // 遍历每个硬币，尝试选择它
        for (int coin : coins) {
            // 如果当前硬币面额大于金额，跳过
            if (amount - coin < 0) continue;

            // 递归计算凑成剩余金额所需的硬币数
            int subProb = helper(coins, amount - coin, memo);

            // 如果无法凑成剩余金额，跳过
            if (subProb == -1) continue;

            // 更新答案
            ans = Math.min(ans, subProb + 1);
        }

        // 记录本轮答案，下标就是凑够当前金额所需的最少硬币数
        memo[amount] = (ans == Integer.MAX_VALUE) ? -1 : ans;
        return memo[amount];
    }

    public static void main(String[] args) {
        CoinChangeMemoization solver = new CoinChangeMemoization();
        int[] coins1 = {1, 2, 5};
        int amount1 = 11;
        System.out.println("最少硬币数（示例1）：" + solver.coinChange(coins1, amount1)); // 输出3

        int[] coins2 = {2};
        int amount2 = 3;
        System.out.println("最少硬币数（示例2）：" + solver.coinChange(coins2, amount2)); // 输出-1

        int[] coins3 = {1, 3, 4};
        int amount3 = 6;
        System.out.println("最少硬币数（示例3）：" + solver.coinChange(coins3, amount3)); // 输出2
    }
}

代码说明：

1. 备忘录初始化：
   • 创建一个长度为 amount+1 的数组 memo，并将所有元素初始化为 -2，表示尚未计算。
   • 设置 memo[0] = 0，因为凑成 0 元需要 0 个硬币。
2. 递归计算：
   • 在 helper 方法中，首先检查当前金额是否为 0，是则返回 0。
   • 然后检查 memo[amount] 是否已计算过，若已计算，直接返回该值。
   • 遍历每个硬币，尝试选择它，递归计算凑成剩余金额所需的硬币数。
   • 更新 ans 为所有可能选择中最小的硬币数。
   • 最后，将计算结果存入备忘录，并返回结果。
3. 时间与空间复杂度：
   • 时间复杂度：O(k*n)，每个子问题（金额）最多被计算一次，且每次计算需遍历 k 种硬币。
   • 空间复杂度：O(n)，用于存储备忘录。

示例输出：

最少硬币数（示例1）：3
最少硬币数（示例2）：-1
最少硬币数（示例3）：2

2-3 动态规划（自底向上）

思路分析：

如果我们有面值为 1 元、3 元和 5 元的硬币若干枚，如何用最少的硬币凑够 11 元？ (表面上这道题可以用贪心算法，但贪心算法无法保证可以求出解，比如 1 元换成 2 元的时候)

如何用最少的硬币凑够i元（i < 11）？ 两个原因：

• 当我们遇到一个大问题时，总是习惯把问题的规模变小，这样便于分析讨论
• 这个规模变小后的问题和原来的问题是同质的，除了规模变小，其它的都是一样的， 本质上它还是同一个问题（规模变小后的问题其实是原问题的子问题）

当 i = 0，即需要多少个硬币来凑够 0 元。 由于 1，3，5 都大于 0，即没有比 0 小的币值，因此凑够 0 元最少需要 0 个硬币。这时候可以用一个 标记 来表示「凑够 0 元最少需要 0 个硬币」。

那么， 我们用 d(i) = j 来表示凑够 i 元最少需要 j 个硬币。于是我们已经得到了 d(0) = 0，表示凑够 0 元最小需要 0 个硬币。

当 i = 1 时，只有面值为 1 元的硬币可用，因此我们拿起一个面值为 1 的硬币，接下来只需要凑够 0 元即可，即 d(0) = 0。所以有：

d(1) = d(1 - 1) + 1 = d(0) + 1 = 0 + 1 = 1

当 i = 2 时，仍然只有面值为 1 的硬币可用，于是我拿起一个面值为 1 的硬币，接下来我只需要再凑够 2 - 1 = 1 元即可， 所以有：

d(2) = d(2 - 1) + 1 = d(1) + 1 = 1 + 1 = 2

当 i = 3 时，我们能用的硬币就有两种了：1 元和 3 元。既然能用的硬币有两种，于是就有两种方案。如果我拿了一个 1 元的硬币，我的目标就变为了： 凑够 3 - 1 = 2 元需要的最少硬币数量。即

d(3) = d(3 - 1) + 1 = d(2) + 1 = 2 + 1 = 3

这个方案说的是，我拿 3 个 1 元的硬币；第二种方案是我拿起一个 3 元的硬币，我的目标就变成：凑够 3 - 3 = 0元需要的最少硬币数量。即

d(3) = d(3 - 3) + 1 = d(0) + 1 = 0 + 1 = 1

这个方案说的是，我拿 1 个 3 元的硬币。

这两种方案哪种更优呢？题目要求使用用最少的硬币数量来凑够 3 元的。所以，选择 d(3) = 1，所以我们得到了 转移状态方程：

d(3) = Math.min(d(3 - 1) + 1, d(3 - 3) + 1);

从以上的文字中， 我们要得到动态规划里非常重要的两个概念：状态 和 状态转移方程。

上文中 d(i) 表示凑够 i 元需要的最少硬币数量，我们将它定义为该问题的 状态， 这个状态是怎么找出来的呢？要根据子问题定义状态，找到子问题，状态也就浮出水面了。最终我们要求解的问题，可以用这个状态来表示：d(11)，即凑够 11 元最少需要多少个硬币。

那状态转移方程是什么呢？既然我们用 d(i) 表示状态，那么状态转移方程应该包含了状态 d(i)，上文中包含状态 d(i) 的方程是：

d(3) = Math.min(d(3 - 1) + 1, d(3 - 3) + 1);

于是它就是状态转移方程，描述状态之间是如何转移的。当然，我们要对它抽象一下，

d(i) = Math.min(d(i), d(i - vj) + 1 ); // 其中 i-vj >= 0，vj 表示第 j 个硬币的面值

所以最终代码：

import java.util.Arrays;

public class CoinChangeDP {
    /**
     * 使用动态规划（自底向上）计算凑成总金额所需的最少硬币数
     * 时间复杂度：O(k*n)，其中 k 是硬币种类数，n 是总金额
     * 空间复杂度：O(n)
     * @param coins 不同面额的硬币数组
     * @param amount 总金额
     * @return 最少的硬币数，如果无法凑成，返回 -1
     */
    public int coinChange(int[] coins, int amount) {
        // 创建 dp 数组，dp[i] 表示凑成 i 元所需的最少硬币数
        // 初始化为 amount + 1，表示无法凑成
        int[] dp = new int[amount + 1];
        Arrays.fill(dp, amount + 1);
        dp[0] = 0; // 凑成 0 元需要 0 个硬币

        // 逐步填充 dp 数组
        for (int i = 1; i <= amount; i++) {
            // 遍历每个硬币
            for (int coin : coins) {
                if (i - coin < 0) {
                    continue; // 如果当前硬币面额大于金额，跳过
                }
                // 更新 dp[i]，取当前值和使用当前硬币后的最小值
                dp[i] = Math.min(dp[i], 1 + dp[i - coin]); // 状态转移方程
            }
        }

        // 如果 dp[amount] 仍为初始值，说明无法凑成目标金额
        return dp[amount] == amount + 1 ? -1 : dp[amount];
    }

    public static void main(String[] args) {
        CoinChangeDP solver = new CoinChangeDP();
        int[] coins1 = {1, 2, 5};
        int amount1 = 11;
        System.out.println("最少硬币数（示例1）：" + solver.coinChange(coins1, amount1)); // 输出3

        int[] coins2 = {2};
        int amount2 = 3;
        System.out.println("最少硬币数（示例2）：" + solver.coinChange(coins2, amount2)); // 输出-1

        int[] coins3 = {1, 3, 4};
        int amount3 = 6;
        System.out.println("最少硬币数（示例3）：" + solver.coinChange(coins3, amount3)); // 输出2
    }
}

代码说明：

1. dp数组定义：
   • dp[i] 表示凑成 i 元所需的最少硬币数。
2. 初始化：
   • 将 dp 数组中的所有元素初始化为 amount + 1，表示初始状态下无法凑成。
   • 设置 dp[0] = 0，因为凑成 0 元需要 0 个硬币。
3. 填表过程：
   • 对于每个金额 i 从 1到 amount：
     • 遍历每个硬币面额 coin：
       • 如果 coin > i，则跳过，因为无法使用该硬币。
       • 否则，更新 dp[i] = Math.min(dp[i], 1 + dp[i - coin])，即比较不使用当前硬币和使用当前硬币后的最小值。
4. 返回结果：
   • 如果 dp[amount] 仍为 amount + 1，说明无法凑成目标金额，返回 -1。
   • 否则，返回 dp[amount]，即最少的硬币数。
5. 时间与空间复杂度：
   • 时间复杂度：O(k*n)，其中 k 是硬币种类数，n 是总金额。
   • 空间复杂度：O(n)，用于存储 dp 数组。

示例输出：

最少硬币数（示例1）：3
最少硬币数（示例2）：-1
最少硬币数（示例3）：2

2-4 动态规划优化（进一步优化）

对于硬币凑钱问题，已经达到了最优的空间复杂度 O(n)。不过，我们可以通过调整循环的顺序，进一步优化程序的运行效率。具体来说，可以将外层循环改为遍历每个硬币，再在内层循环中遍历金额，这样有助于减少不必要的计算。

import java.util.Arrays;

public class CoinChangeOptimizedDP {
    /**
     * 使用动态规划（自底向上）优化版本计算凑成总金额所需的最少硬币数
     * 时间复杂度：O(k*n)，其中 k 是硬币种类数，n 是总金额
     * 空间复杂度：O(n)
     * @param coins 不同面额的硬币数组
     * @param amount 总金额
     * @return 最少的硬币数，如果无法凑成，返回 -1
     */
    public int coinChange(int[] coins, int amount) {
        // 创建 dp 数组，dp[i] 表示凑成 i 元所需的最少硬币数
        // 初始化为 amount + 1，表示无法凑成
        int[] dp = new int[amount + 1];
        Arrays.fill(dp, amount + 1);
        dp[0] = 0; // 凑成 0 元需要 0 个硬币

        // 遍历每个硬币，逐步更新 dp 数组
        for (int coin : coins) {
            for (int i = coin; i <= amount; i++) {
                dp[i] = Math.min(dp[i], dp[i - coin] + 1); // 状态转移方程
            }
        }

        // 如果 dp[amount] 仍为初始值，说明无法凑成目标金额
        return dp[amount] == amount + 1 ? -1 : dp[amount];
    }

    public static void main(String[] args) {
        CoinChangeOptimizedDP solver = new CoinChangeOptimizedDP();
        int[] coins1 = {1, 2, 5};
        int amount1 = 11;
        System.out.println("最少硬币数（示例1）：" + solver.coinChange(coins1, amount1)); // 输出3

        int[] coins2 = {2};
        int amount2 = 3;
        System.out.println("最少硬币数（示例2）：" + solver.coinChange(coins2, amount2)); // 输出-1

        int[] coins3 = {1, 3, 4};
        int amount3 = 6;
        System.out.println("最少硬币数（示例3）：" + solver.coinChange(coins3, amount3)); // 输出2
    }
}

代码说明：

1. 优化策略：
   • 外层循环遍历每个硬币，内层循环遍历金额。这种顺序有助于减少不必要的计算，因为每个硬币都只会影响特定的金额范围。
2. 填表过程：
   • 对于每个硬币coin：
     • 遍历金额 i 从 coin 到 amount：
       • 更新 dp[i] = Math.min(dp[i], 1 + dp[i - coin])，即比较不使用当前硬币和使用当前硬币后的最小值。
3. 时间与空间复杂度：
   • 时间复杂度：O(k*n)，其中 k 是硬币种类数，n 是总金额。
   • 空间复杂度：O(n)，用于存储 dp 数组。

示例输出：

最少硬币数（示例1）：3
最少硬币数（示例2）：-1
最少硬币数（示例3）：2

进一步优化说明：

这种优化方法充分利用了状态转移方程的特性，只保留了与当前状态相关的前两项，显著降低了空间复杂度。同时，通过调整循环的顺序，确保每个硬币的影响范围明确，减少了不必要的更新操作，从而提升了程序的运行效率。

5. 动态规划与其他算法比较

• 分治法：当子问题独立时适合用分治；若子问题重叠多，则可能时间开销大。
• 贪心算法：在每一步都作出局部最优选择，但不一定能保证全局最优；DP需要子问题最优解也能构成整体最优解（最优子结构）。
• 回溯算法：通常适合搜索或枚举场景，时间复杂度往往较高。若有大量重复子问题，DP能通过记忆化大幅优化。