算法思想 - 优先遍历算法

1. 深度优先遍历（DFS）

深度优先（Depth First Search, DFS）遍历是一种典型的搜索方法，其核心思想是沿着一个方向尽可能深入，直到无法继续时再回退到上一个分叉点，然后探索未访问的分支。 DFS 有两种常见实现方式：递归实现 和 迭代实现（使用栈模拟递归过程）。

1.1 深度优先遍历的特点

1. 深入优先：每次优先访问当前节点的子节点，直到到达叶子节点（无子节点）。
2. 回溯：当某条路径走不通时，回退到最近的分叉点继续探索其他未访问的分支。
3. 应用广泛：适用于图的遍历、树的遍历（如前序、中序、后序遍历）以及许多搜索问题。

---

以下图为例，节点按照以下顺序连接： 节点 1 与 2, 3, 4 相连，2 与 5 相连，3 与 6, 7 相连，5 与 9 相连，6 与 10 相连。

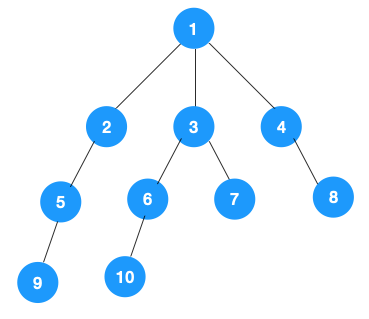
遍历过程：

1. 从根节点 1 开始，先访问节点 2，然后递归进入其子节点 5。
2. 再递归访问 5 的子节点 9。
3. 当 9 没有子节点时回溯到 5，再回溯到 2，回到根节点 1。
4. 接着访问节点 3 的子节点 6，进入 10，完成后回溯到 6，然后到 3 的下一个子节点 7。
5. 最后回到根节点 1，探索节点 4 及其子节点 8。

完整的遍历顺序为：1 -> 2 -> 5 -> 9 -> 3 -> 6 -> 10 -> 7 -> 4 -> 8。

完整遍历图：

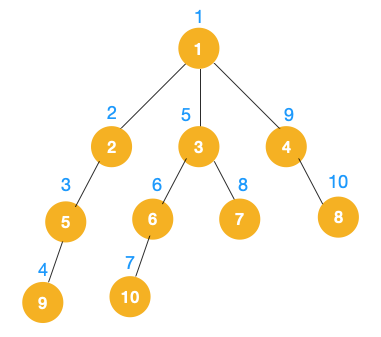
动图描述（利用栈实现）：

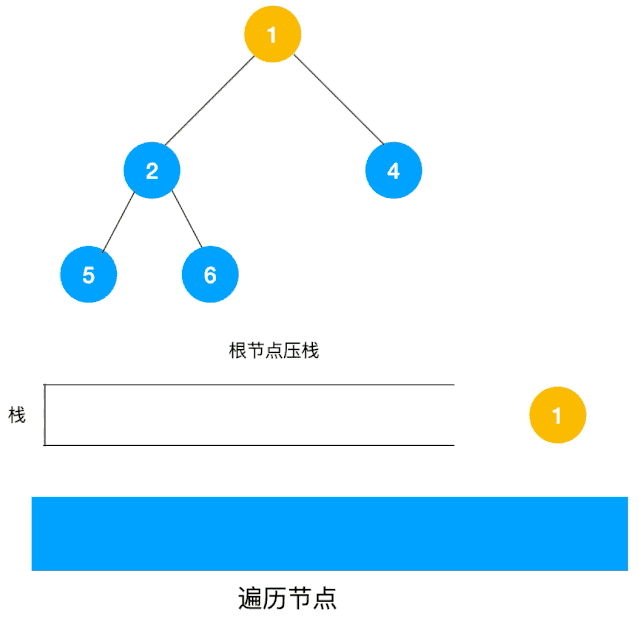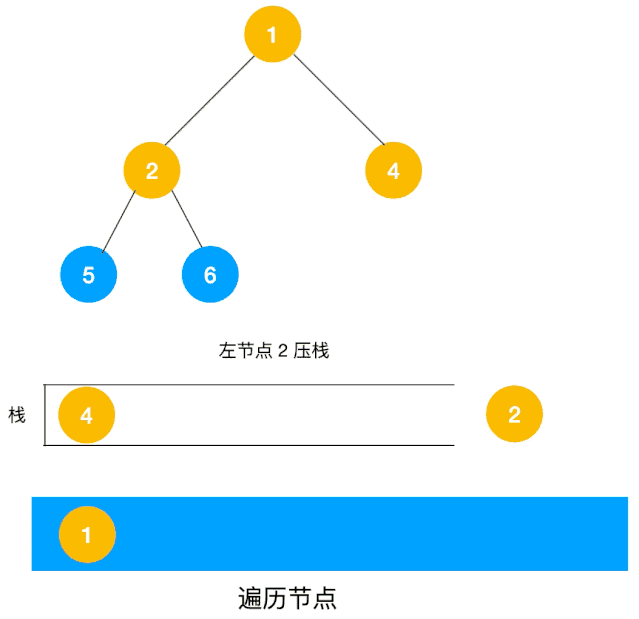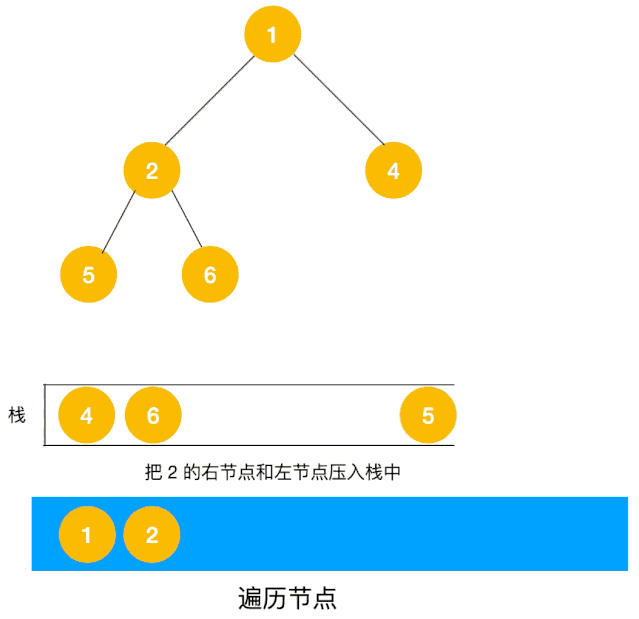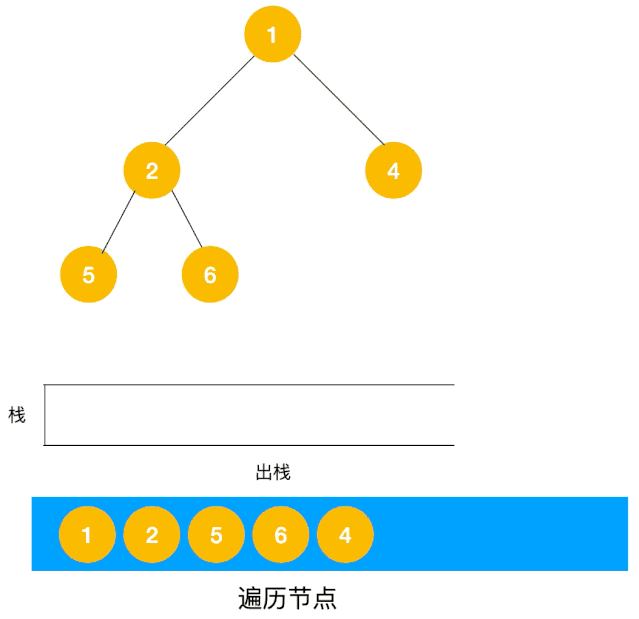
1.2 深度优先遍历的实现

递归实现

思路：

1. 从根节点开始访问。
2. 对于每个节点：
   • 先访问当前节点；
   • 然后递归访问其左子节点；
   • 最后递归访问其右子节点。
3. 当到达叶子节点（无子节点）时终止递归。

public static void dfsRecursive(TreeNode root) {
    if (root == null) { // 递归终止条件
        return;
    }
    System.out.print("DFS 遍历节点：" + root.val + " ");
    // 递归访问左子节点
    dfsRecursive(root.left);
    // 递归访问右子节点
    dfsRecursive(root.right);
}

---

迭代实现（基于栈）

思路：

1. 使用栈（LIFO）模拟递归过程。
2. 将根节点压入栈。
3. 在每次循环中，弹出栈顶节点并访问：
   • 先将右子节点压入栈；
   • 再将左子节点压入栈（确保左子节点优先访问）。
4. 栈为空时遍历完成。

import java.util.Stack;

public static void dfsIterative(TreeNode root) {
    if (root == null) {
        return;
    }
    Stack<TreeNode> stack = new Stack<>(); // 用栈实现深度优先遍历
    stack.push(root); // 初始化将根节点压入栈
    while (!stack.isEmpty()) { // 当栈非空时
        TreeNode node = stack.pop(); // 弹出栈顶节点
        System.out.print("DFS 遍历节点：" + node.val + " ");
        // 先压入右子节点，再压入左子节点
        if (node.right != null) {
            stack.push(node.right);
        }
        if (node.left != null) {
            stack.push(node.left);
        }
    }
}

不难发现，上面的图这就是树的前序遍历，实际上不管是前序遍历，还是中序遍历，亦或是后序遍历，都属于深度优先遍历。

详细关于 DFS 的前序遍历、中序遍历、后序遍历的讲解，请看 算法模板 - 二叉树遍历 (opens new window)。

1.3 深度优先遍历的优点

• 内存使用效率高：一次只存储当前路径上的节点。
• 适用于解决路径搜索类问题，如：迷宫求解、岛屿计数问题等。

实现对比：

实现方式	优点	缺点
递归	代码简洁，直观易懂	深度过大可能导致栈溢出
迭代	可避免递归栈溢出问题	需要手动维护栈，稍显繁琐

2. 广度优先遍历（BFS）

广度优先遍历（Breadth First Search, BFS）是一种按照 层次 遍历的方法，从根节点开始，一层一层地向下访问树或图中的所有节点。在每一层中，所有节点会按照从左到右的顺序被访问，直到所有节点都被遍历。

2.1 广度优先遍历的特点

1. 层次性：从根节点开始，依次访问其所有直接子节点，然后访问这些子节点的子节点，以此类推。
2. 利用队列：BFS 需要一个 队列 来存储当前层的节点。
3. 访问顺序：先访问当前层，再访问下一层，确保每一层的节点在前一层的节点被完全访问后才被访问。

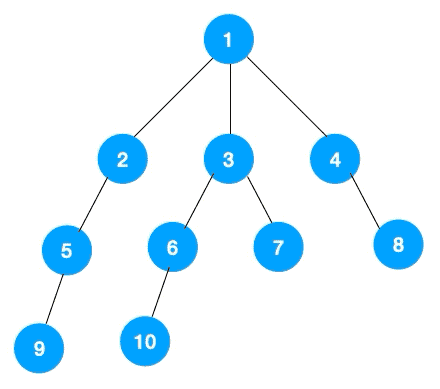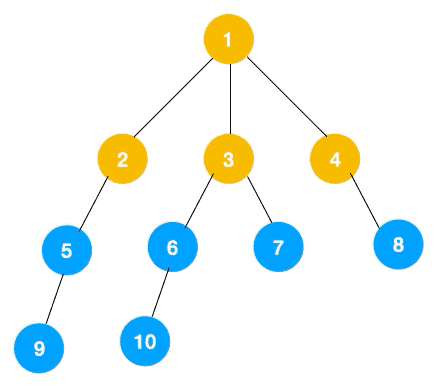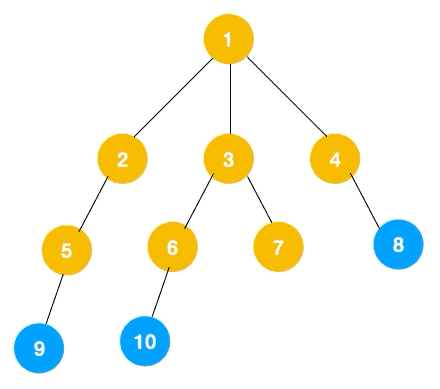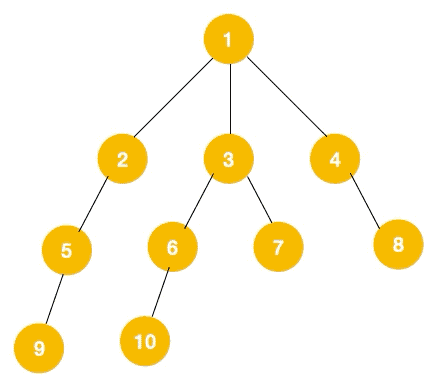
广度优先遍历的顺序如下：

1. 首先访问根节点 1；
2. 接着访问第二层的节点 2, 3, 4；
3. 然后访问第三层的节点 5, 6, 7, 8；
4. 最后访问第四层的节点 9, 10。

如下动图所示：

2.2 利用队列实现 BFS

BFS 使用队列来存储当前层的节点。在队列中，每次从队首取出节点，将其子节点加入队列，然后继续处理队首节点，直到队列为空。 如下动图所示：

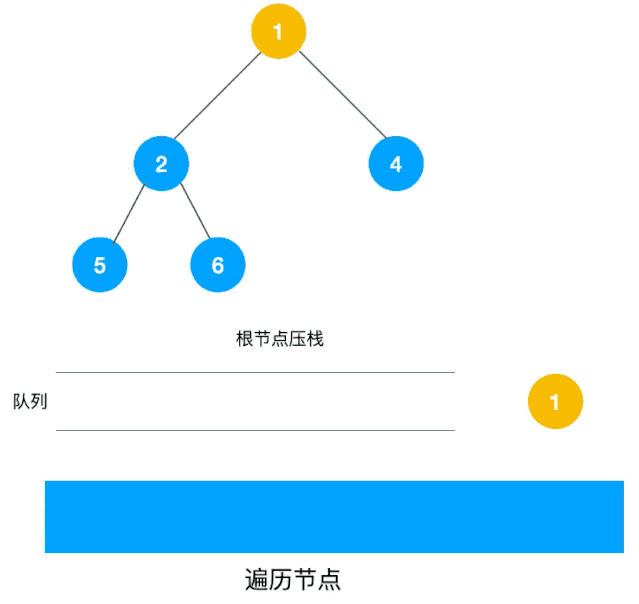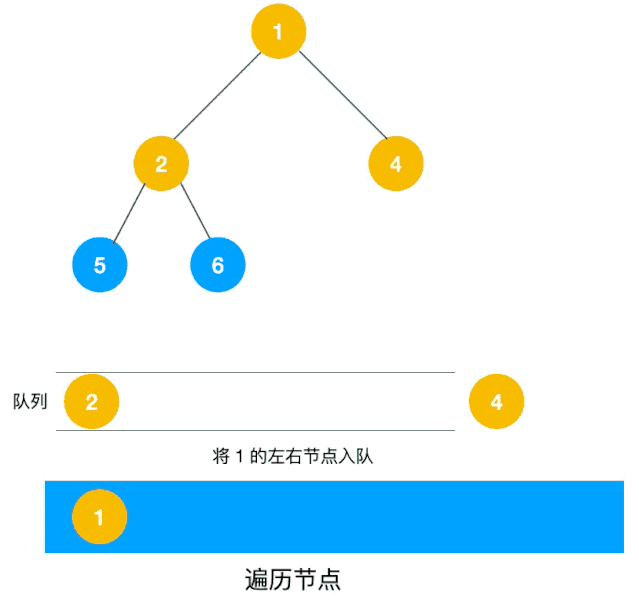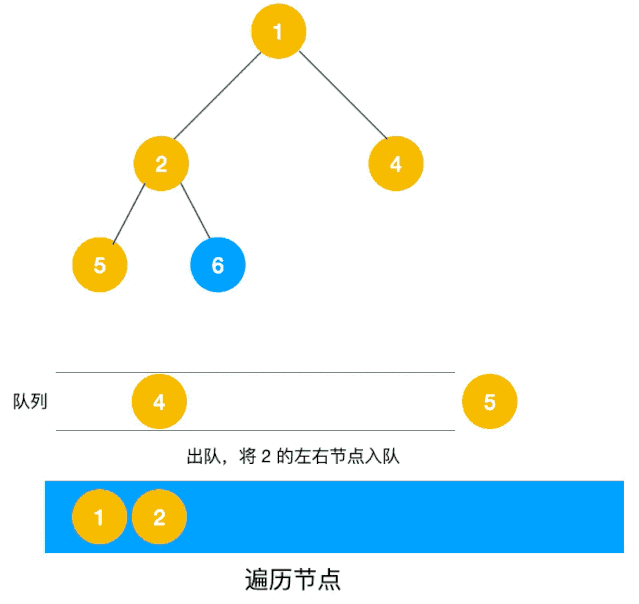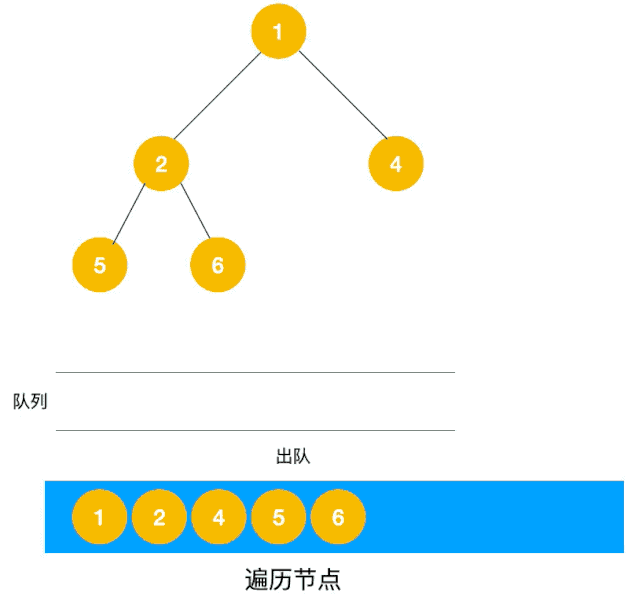
1. 使用一个队列来维护待访问节点：
   • 初始化时，将根节点加入队列。
   • 在每次循环中，从队列中取出队首节点，处理该节点的值（打印或存储）。
   • 然后将该节点的子节点依次加入队列。
2. 当队列为空时，所有节点都已被访问，遍历结束。

import java.util.LinkedList;
import java.util.Queue;

public class BFS {
    public static void bfs(Node root) {
        if (root == null) { // 边界条件
            return;
        }

        // 使用队列存储当前层的节点
        Queue<Node> queue = new LinkedList<>();
        queue.add(root); // 将根节点加入队列

        // 遍历直到队列为空
        while (!queue.isEmpty()) {
            Node node = queue.poll(); // 从队首取出节点
            System.out.println("BFS 遍历节点：" + node.val);

            // 将子节点加入队列
            if (node.left != null) {
                queue.add(node.left);
            }
            if (node.right != null) {
                queue.add(node.right);
            }
        }
    }
}

2.3 广度优先遍历的应用

BFS 不仅适用于树的遍历，还广泛应用于图的遍历和路径搜索问题。典型应用包括：

1. 最短路径问题：在无权图中，BFS 可找到从起点到终点的最短路径。
2. 层次遍历：用于打印树的每一层。
3. 连通性检测：判断图是否连通。

2.4 深度优先遍历与广度优先遍历对比

特点	深度优先遍历（DFS）	广度优先遍历（BFS）
核心数据结构	栈（递归隐式栈或显式栈）	队列
访问顺序	先深入再回溯	一层一层访问
适用场景	路径搜索、连通性检测	层次遍历、最短路径问题
实现难度	简单（递归实现较直观）	较简单
空间复杂度	O(h)O(h)（树的高度或图的深度）	O(w)O(w)（树的最大宽度）