面试
刷题笔记

链表系列

1. 合并两个有序链表
2. 分割链表
3. 合并k个有序链表
4. 链表中倒数第k个结点
5. 删除链表的倒数第 N 个结点
6. 链表的中间节点
7. 环形链表
8. 环形链表||
9. 相交链表
10. 反转链表
11. 反转链表||
12. K个一组翻转链表
13. 回文链表
14. 移除链表元素
15. 两两交换链表中的节点

# 1. 合并两个有序链表

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

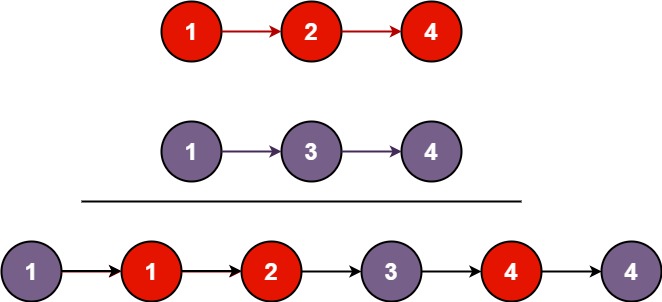
输入：l1 = [1,2,4], l2 = [1,3,4]

输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []

输出：[]

示例 3：

输入：l1 = [], l2 = [0]

输出：[0]

提示：

两个链表的节点数目范围是 [0, 50]
-100 <= Node.val <= 100
l1 和 l2 均按 非递减顺序 排列

解题思路如下：力扣链接 (opens new window)

处理特殊情况：
如果任一链表为空，则返回另一链表作为合并后的链表。

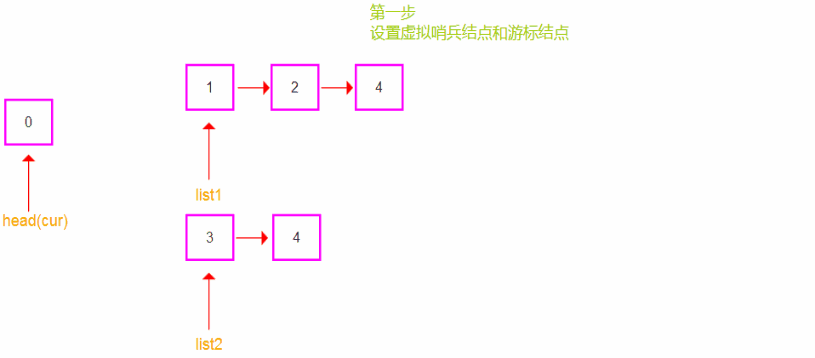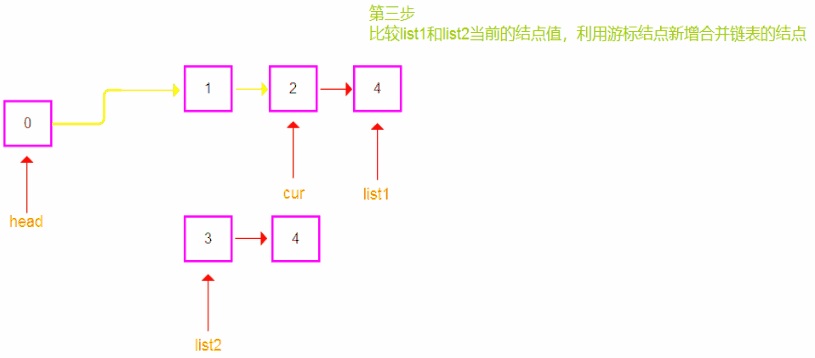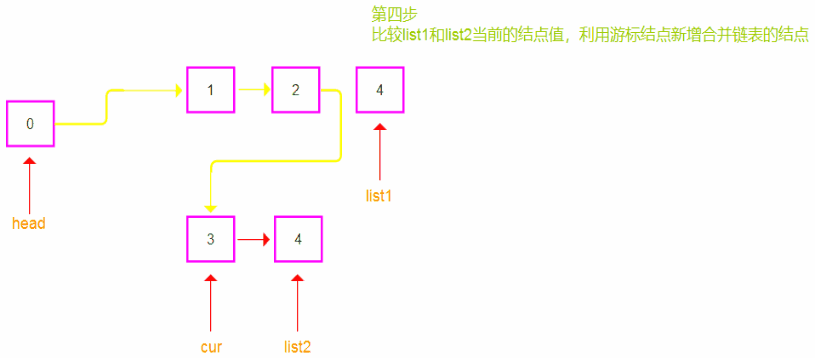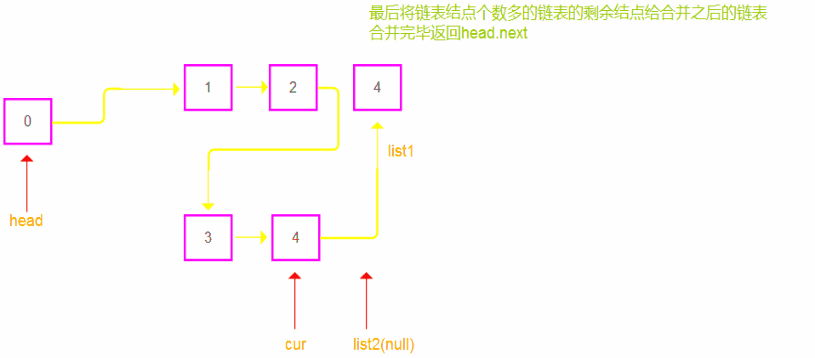
如果两个链表都为空，返回null。

设置哨兵结点：
创建一个虚拟哨兵节点head，它的作用是为了简化在头节点前插入节点的操作。我们将在其后添加所有排序后的节点。

使用游标节点cur来追踪合并链表的最后一个节点的位置。

遍历两个链表：
同时遍历两个链表，比较当前两个链表节点的值。

将较小值的节点连接到合并链表的最后，并移动当前链表的指针和游标节点cur。

处理剩余节点：
一旦其中一个链表的节点都被遍历完，将另一个链表剩余的所有节点直接连接到合并链表的最后。

返回合并后的链表：
合并完成后，返回哨兵节点head的下一个节点，即合并后链表的头节点。

时间复杂度为O(n+m)，其中n是链表1的长度，m是链表2的长度。

双指针解题代码如下

class Solution {
    public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
     //三种特殊情况   
     if(list1 == null) return list2; //链表一为空，则合并之后的链表为链表二
     if(list2 == null) return list1; //链表二为空，则合并之后的链表为链表一
     if(list1 == null && list2 == null) return null; //两个链表都为空，则合并之后的链表也为空
 
     // 创建虚拟哨兵节点和游标节点
     ListNode head = new ListNode();  // 虚拟哨兵节点
     ListNode cur = head; //游标结点
        
     // 遍历两个链表，直到其中一个为空   
     while(list1 != null && list2 != null) {
	// 如果链表一的当前节点小于链表二的当前节点
        // 将链表一的当前节点添加到合并链表中         
        if(list1.val < list2.val) { 
            cur.next = list1;
            list1 = list1.next;  // 移动链表一的指针
        }else {     
            // 否则将链表二的当前节点添加到合并链表中
            cur.next = list2;
            list2 = list2.next;  // 移动链表二的指针
        }
        cur = cur.next; // 移动游标节点
     }
        
     // 处理剩余节点
     if(list1 != null){
         cur.next = list1; // 链表一剩余节点直接接在合并链表的末尾
     }
 
     if(list2 != null){
         cur.next = list2; // 链表二剩余节点直接接在合并链表的末尾
     }
     return head.next; // 返回合并后的链表头节点（跳过虚拟头节点）
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

# 2. 分割链表

给你一个链表的头节点 head 和一个特定值 x ，请你对链表进行分隔，使得所有小于 x 的节点都出现在 大于或等于 x 的节点之前。

你应当保留两个分区中每个节点的初始相对位置。

示例 1：

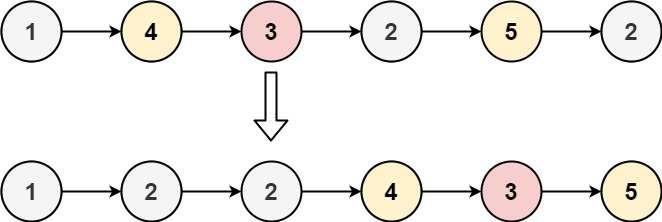
输入：head = [1,4,3,2,5,2], x = 3

输出：[1,2,2,4,3,5]

示例 2：

输入：head = [2,1], x = 2

输出：[1,2]

提示：

链表中节点的数目在范围 [0, 200] 内
-100 <= Node.val <= 100
-200 <= x <= 200

解题思路如下：力扣链接 (opens new window)

如下图所示，题目要求实现链表所有「值 <x 节点」出现在「值 ≥x 节点」前面。

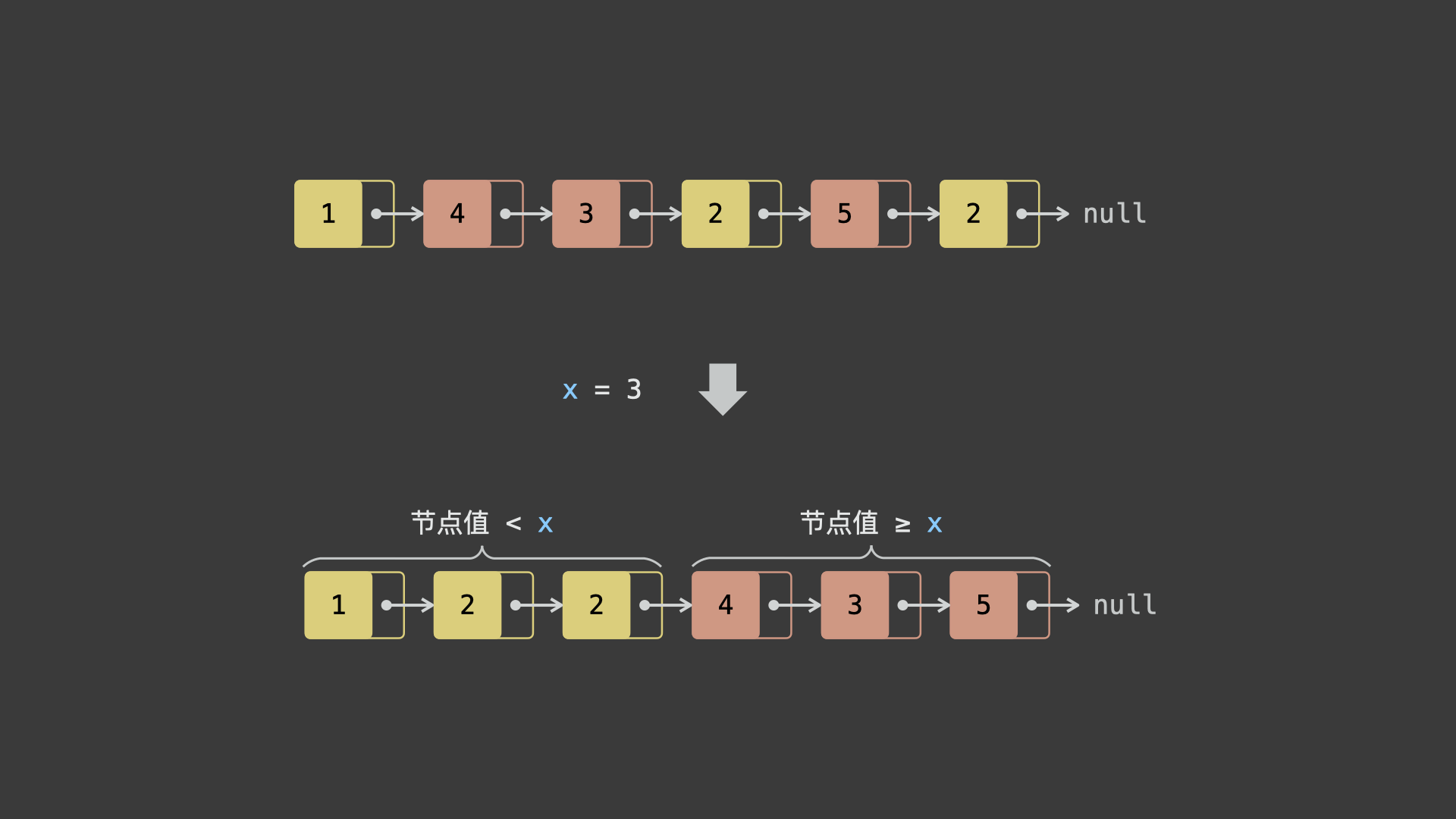
ccw-02-04.001.png

根据题意，考虑通过「新建两个链表」实现原链表分割，算法流程为：

新建两个链表 sml_dummy , big_dummy ，分别用于添加所有【节点值 <x】、【节点值 ≥x】的节点。

遍历链表 head 并依次比较各节点值 head.val 和 xxx 的大小：
若 head.val < x ，则将节点 head 添加至链表 sml_dummy 最后面；

若 head.val >= x ，则将节点 head 添加至链表 big_dummy 最后面；

遍历完成后，拼接 sml_dummy 和 big_dummy 链表。

最终返回头节点 sml_dummy.next 即可。

时间复杂度是O(n)，其中n是链表的长度。这是因为每个节点都需要被访问和比较一次。

双指针解题代码如下

class Solution {
    public ListNode partition(ListNode head, int x) {
        // 创建两个虚拟头结点，分别用于链接小于x和大于等于x的节点
        ListNode smlDummy = new ListNode(0), bigDummy = new ListNode(0);
        // 初始化游标指针，分别指向两个链表的尾部
        ListNode sml = smlDummy, big = bigDummy;
        
        // 遍历原始链表
        while (head != null) {
            // 判断当前节点的值与x的大小，将节点添加到对应的链表
            if (head.val < x) {
                sml.next = head; // 小于x的节点加入到sml链表
                sml = sml.next; // 移动sml指针
            } else {
                big.next = head; // 大于等于x的节点加入到big链表
                big = big.next; // 移动big指针
            }
            head = head.next; // 继续遍历下一个节点
        }
        
        // 连接小链表和大链表
        sml.next = bigDummy.next; // 将大链表接在小链表的末尾
        big.next = null; // 处理尾部空节点，防止循环引用
        
        return smlDummy.next; // 返回合并后的链表头节点
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 3. 合并k个有序链表

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]

输出：[1,1,2,3,4,4,5,6]

解释：链表数组如下：

[

1->4->5,

1->3->4,

2->6

] 将它们合并到一个有序链表中得到。

1->1->2->3->4->4->5->6

示例 2：

输入：lists = []

输出：[]

示例 3：

输入：lists = [[]]

输出：[]

提示：

k == lists.length
0 <= k <= 10^4
0 <= lists[i].length <= 500
-10^4 <= lists[i][j] <= 10^4
lists[i] 按升序排列
lists[i].length 的总和不超过 10^4

解题思路如下：力扣链接 (opens new window)

合并k个有序链表的问题本质上是一个多路归并问题。我们的目标是从k个链表中的所有节点构建一个单一的、全局有序的链表。直观的解决方法可能是一次处理一个节点，但这会涉及到频繁的比较操作，特别是当k的值较大时，效率会非常低下。为了优化这个过程，我们引入了优先级队列（二叉堆），来帮助我们高效地找到当前k个链表中值最小的节点。

最小堆的使用：
在任何时刻，我们都需要从k个链表中找到当前值最小的节点。最小堆是一个完美的数据结构，可以在O(logk)的时间内进行插入和删除最小元素操作，远远快于O(k)的线性查找。

我们将k个链表的头节点放入最小堆中。堆顶元素即是这些头节点中最小的一个。

分步处理和合并：
初始化：先将每个链表的头结点（如果非空）加入到最小堆中。这样堆顶就是所有头结点中最小的那个。

迭代合并：然后我们进入一个循环，每次循环中：
从堆中取出堆顶元素，即当前最小的节点，将其添加到合并后的链表中。

如果这个最小节点还有下一个节点，将下一个节点也放入堆中。这样做是因为下一个节点是下一轮可能的最小值候选。

每次从堆中取出一个节点后，我们都将新节点（即刚取出节点的下一个节点）放入堆中，保持堆的大小不变，始终为k或更小（当某个链表被完全弹出时）。

循环结束条件：当堆为空时，所有链表的节点都已经被处理完毕，循环结束。

保留节点的相对顺序：
每次我们都是取当前k个节点中最小的节点加入到结果链表中，这自然地保持了原链表内部节点的相对顺序，因为我们每次只取一个链表的头部节点加入到结果链表，并且在取出节点后，我们会将该节点的下一节点加入堆中等待下次比较。

构建完整的合并链表：
使用一个虚拟头结点来简化边界情况处理，可以避免在合并链表时处理空链表的特殊情况。

通过不断从优先级队列中弹出节点并将节点的下一节点加入队列，我们能够逐步构建出完整的合并后链表。

优先级队列解题代码如下

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        if (lists.length == 0) return null; // 特殊情况处理

        // 创建虚拟头结点和游标节点的指针
        ListNode dummy = new ListNode(-1);  // 虚拟头结点
        ListNode cur = dummy; // 游标节点，用于连接结果链表的指针
        
        // 创建优先级队列（最小堆），按节点值大小排列
        PriorityQueue<ListNode> pq = new PriorityQueue<>(
            lists.length, (a, b)->(a.val - b.val));
        
        // 将每个链表的头结点加入最小堆
        for (ListNode head : lists) {
            if (head != null) pq.add(head);
        }

        while (!pq.isEmpty()) {
            // 获取最小节点，接到结果链表中
            ListNode node = pq.poll(); // 弹出最小节点
            cur.next = node; // 连接到合并后的链表
            if (node.next != null) {
                pq.add(node.next); // 如果最小节点还有下一个节点，加入最小堆中
            }
            cur= cur.next; // 移动指针到合并链表的末尾
        }
        return dummy.next; // 返回合并后的链表头节点
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

# 4. 链表中倒数第k个结点

描述

输入一个链表，输出该链表中倒数第k个结点。

示例1

输入：1,{1,2,3,4,5}

返回值：{5}

解题思路如下：力扣链接 (opens new window)

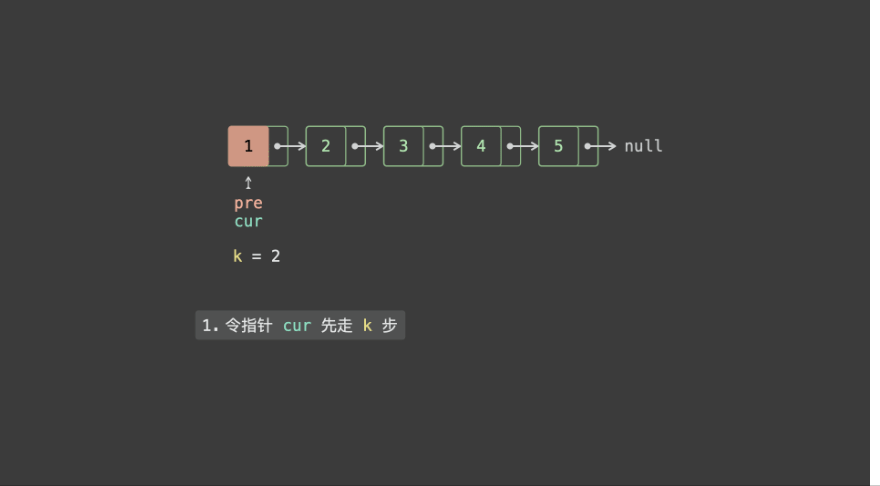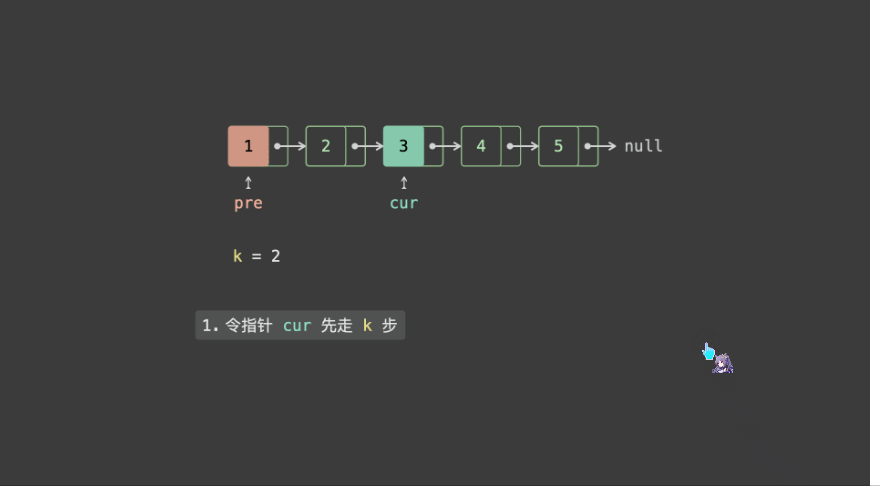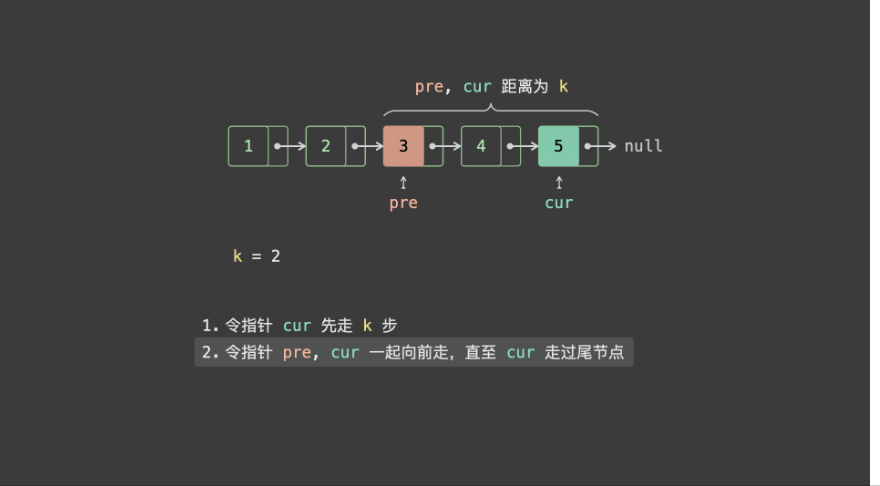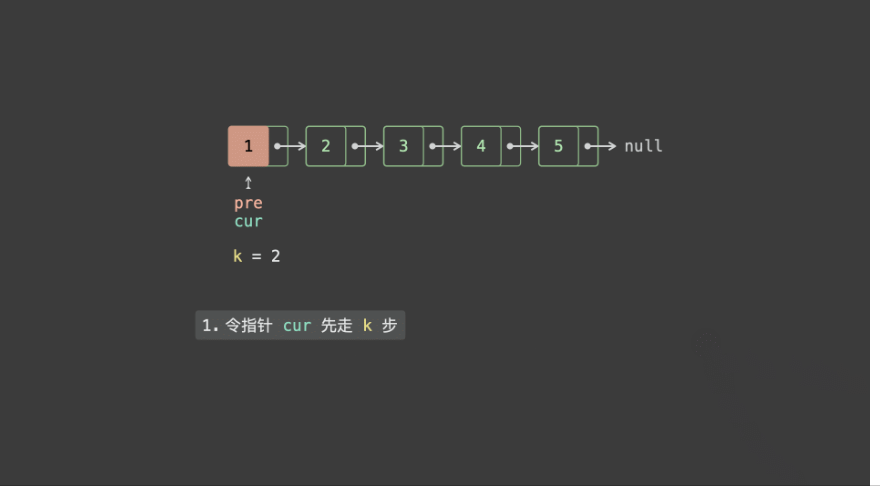
初始化双指针 pre , cur 都指向头节点 head ；

先令 cur 走 k步，此时 pre , cur 的距离为 k；

令 pre , cur 一起走，直到 cur 走过尾节点时跳出，此时 pre 指向「倒数第 kkk 个节点」，返回之即可；

时间复杂度为O(n)，无论如何，这个算法都需要遍历整个链表一次

双指针解题代码如下

ListNode findFromEnd(ListNode head, int k) {
    ListNode cur = head;
    // cur 先走 k 步
    for (int i = 0; i < k; i++) {
        cur = cur.next;
    }
    ListNode pre = head;
    // pre 和 cur 同时走 n - k 步
    while (cur != null) {
        pre = pre.next;
        cur = cur.next;
    }
    // pre 现在指向第 n - k + 1 个节点，即倒数第 k 个节点
    return pre;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 5. 删除链表的倒数第 N 个结点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：

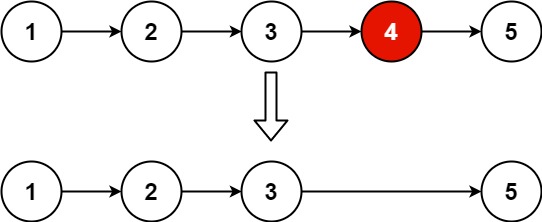
输入：head = [1,2,3,4,5], n = 2

输出：[1,2,3,5]

示例 2：

输入：head = [1], n = 1

输出：[]

示例 3：

输入：head = [1,2], n = 1

输出：[1]

提示：

链表中结点的数目为 sz
1 <= sz <= 30
0 <= Node.val <= 100
1 <= n <= sz

解题思路如下：力扣链接 (opens new window)

删除倒数第 n 个，我们只需要找倒数第 n + 1 个节点（详情见上题），更改这个节点下一个地址的指向即可

通过引入虚拟头结点，我们在原始链表的前面人为添加了一个额外的节点，这样无论是需要删除原始头节点还是其他节点，待删除节点的前一个节点总是存在的。这就简化了逻辑，我们总是可以通过pre.next指向待删除节点，然后执行pre.next = pre.next.next来删除倒数第n个节点。这样避免了针对头节点特殊处理的需求，同时也避免了空指针的问题，使得代码更加简洁和健壮。

时间复杂度O(n)，主要的时间开销来自于遍历链表以找到倒数第n+1个节点

双指针解题代码如下

// 主函数
public ListNode removeNthFromEnd(ListNode head, int n) {
    // 虚拟头结点
    ListNode dummy = new ListNode(-1);
    dummy.next = head;
    // 删除倒数第 n 个，要先找倒数第 n + 1 个节点
    ListNode pre = findFromEnd(dummy, n + 1);
    // 删掉倒数第 n 个节点
    pre.next = pre.next.next;
    return dummy.next;
}
// 寻找链表的倒数第 n+1 个节点
private ListNode findFromEnd(ListNode head, int k) {
    ListNode cur = head;
    // cur 先走 k 步
    for (int i = 0; i < k; i++) {
        cur = cur.next;
    }
    ListNode pre = head;
    // pre 和 cur 同时走 n - k 步
    while (cur != null) {
        pre = pre.next;
        cur = cur.next;
    }
    // pre 现在指向第 n - k + 1 个节点，即倒数第 k 个节点
    return pre;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 6. 链表的中间节点

给你单链表的头结点 head ，请你找出并返回链表的中间结点。

如果有两个中间结点，则返回第二个中间结点。

示例 1：

输入：head = [1,2,3,4,5]

输出：[3,4,5]

解释：链表只有一个中间结点，值为 3 。

示例 2：

输入：head = [1,2,3,4,5,6]

输出：[4,5,6]

解释：该链表有两个中间结点，值分别为 3 和 4 ，返回第二个结点。

提示：

链表的结点数范围是 [1, 100]
1 <= Node.val <= 100

解题思路如下：力扣链接 (opens new window)

这道题的关键在于我们无法直接得到单链表的长度 n，常规方法是先遍历链表计算 n，再遍历一次得到第 n / 2 个节点，也就是中间节点。

如果想一次遍历就得到中间节点，也需要耍点小聪明，使用「快慢指针」的技巧：

我们让两个指针 slow 和 fast 分别指向链表头结点 head。

每当慢指针 slow 前进一步，快指针 fast 就前进两步，这样，当 fast 走到链表末尾时，slow 就指向了链表中点。

慢指针走一步，快指针走两步。这里分两种情况。

情况一：当链表结点个数为偶数时，快指针为null结束遍历

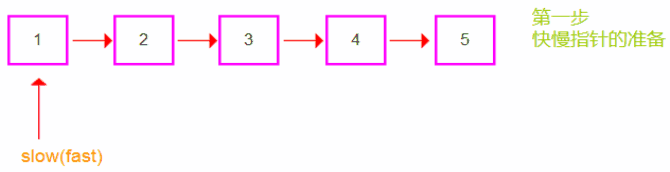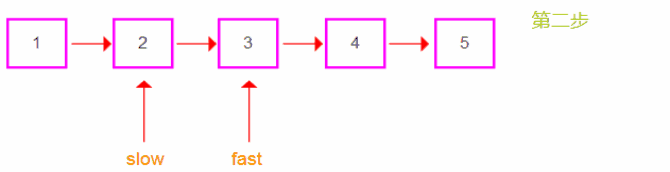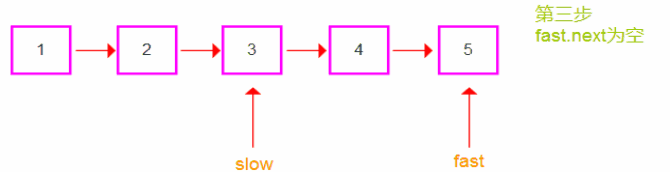
情况二：当链表结点个数为奇数时，快指针的next域为空结束遍历。

情况一过程展示

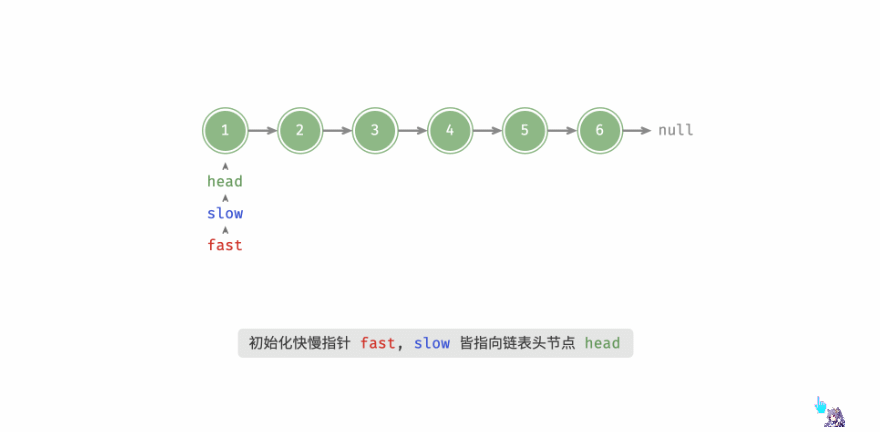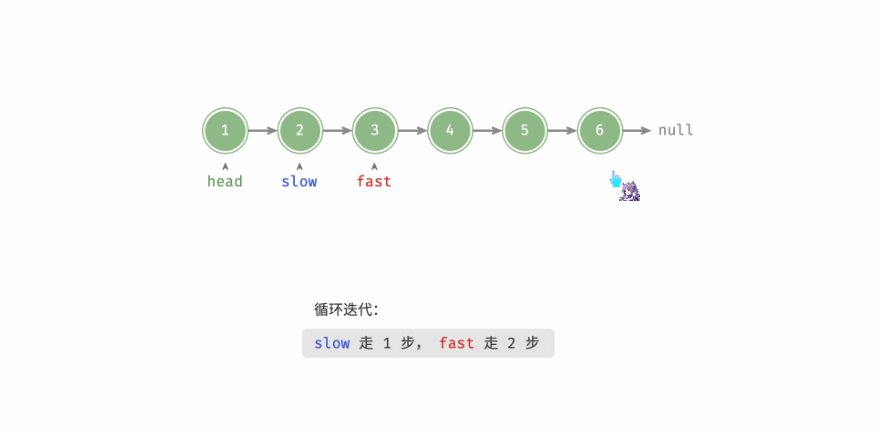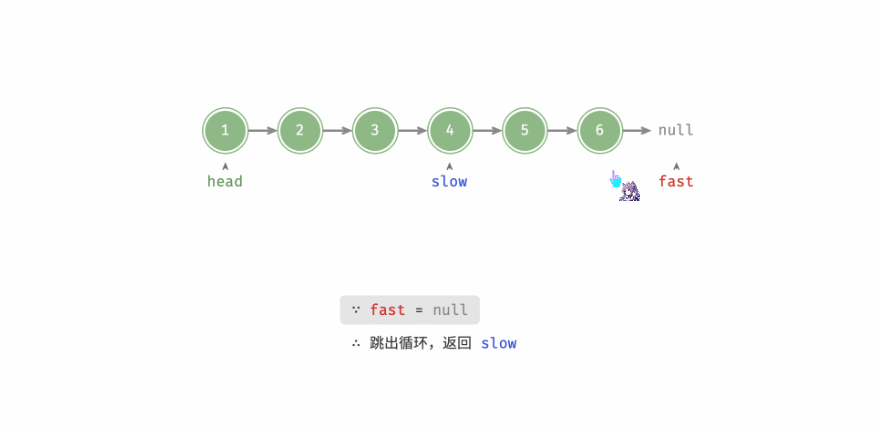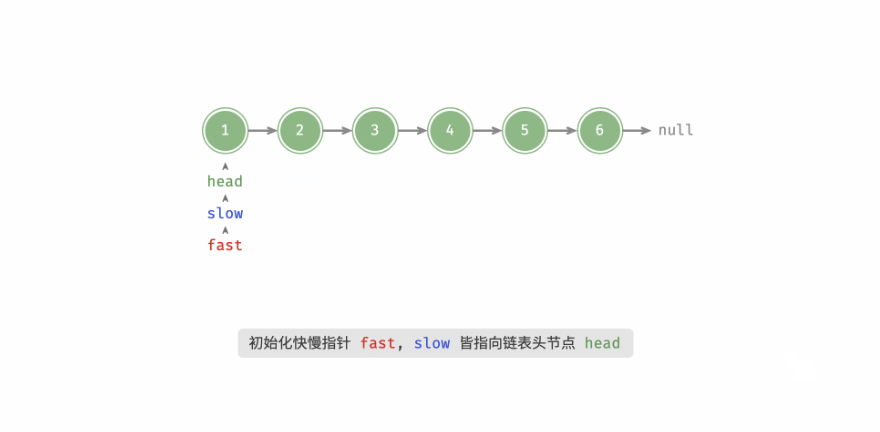
情况二过程展示

快慢指针解题代码如下

class Solution {
    public ListNode middleNode(ListNode head) {
        //如果链表为空或只有一个结点都返回它本身
        if(head == null || head.next == null) return head;
 
        // 快慢指针初始化指向 head
        ListNode slow = head; //慢指针
        ListNode fast = head;  //快指针
        while(fast != null && fast.next != null) {
            slow = slow.next; //慢指针走一步
            fast = fast.next.next; //快指针走两步
        }
        return slow;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 7. 环形链表

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。否则，返回 false 。

示例 1：

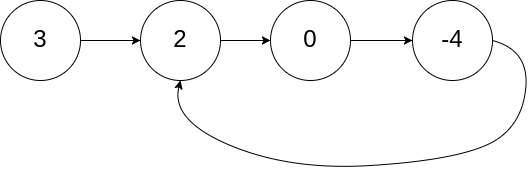
输入：head = [3,2,0,-4], pos = 1

输出：true

解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

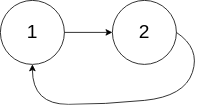
输入：head = [1,2], pos = 0 输出：true 解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1 输出：false 解释：链表中没有环。

提示：

链表中节点的数目范围是 [0, 104]
-105 <= Node.val <= 105
pos 为 -1 或者链表中的一个 有效索引 。

解题思路如下：力扣链接 (opens new window)

快慢指针：慢指针走一步，快指针走两步。

快指针每次比慢指针多走一步，意味着快指针是一步一步接近慢指针的

如果 fast 最终遇到空指针，说明链表中没有环；如果 fast 最终和 slow 相遇，那肯定是 fast 超过了 slow 一圈，说明链表中含有环。

时间复杂度是O(N)，其中N是链表中节点的数量。这是因为无论链表是否有环，最多只会遍历每个节点一次

快慢指针解题代码如下

boolean hasCycle(ListNode head) {
    // 快慢指针初始化指向 head
    ListNode slow = head, fast = head;
    // 快指针走到末尾时停止
    while (fast != null && fast.next != null) {
        // 慢指针走一步，快指针走两步
        slow = slow.next;
        fast = fast.next.next;
        // 快慢指针相遇，说明含有环
        if (slow == fast) {
            return true;
        }
    }
    // 不包含环
    return false;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 8. 环形链表||

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

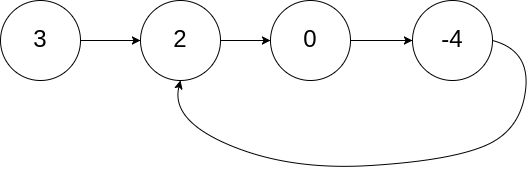
输入：head = [3,2,0,-4], pos = 1

输出：返回索引为 1 的链表节点

解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0

输出：返回索引为 0 的链表节点

解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1

输出：返回 null

解释：链表中没有环。

提示：

链表中节点的数目范围在范围 [0, 104] 内
-105 <= Node.val <= 105
pos 的值为 -1 或者链表中的一个有效索引

解题思路如下：力扣链接 (opens new window)

快慢指针：慢指针走一步，快指针走两步。

如果快指针和慢指针最后相遇，则链表中存在环，不存在环直接返回null，将慢指针恢复到原始链表的头，fast在链表环中它们的相遇点，两个指针同时(慢指针和快指针都一步一步地走)行走，再次相遇点就是链表开始入环的第一个节点。

这道题需要推导出一个公式：看完图解基本上就能懂了：

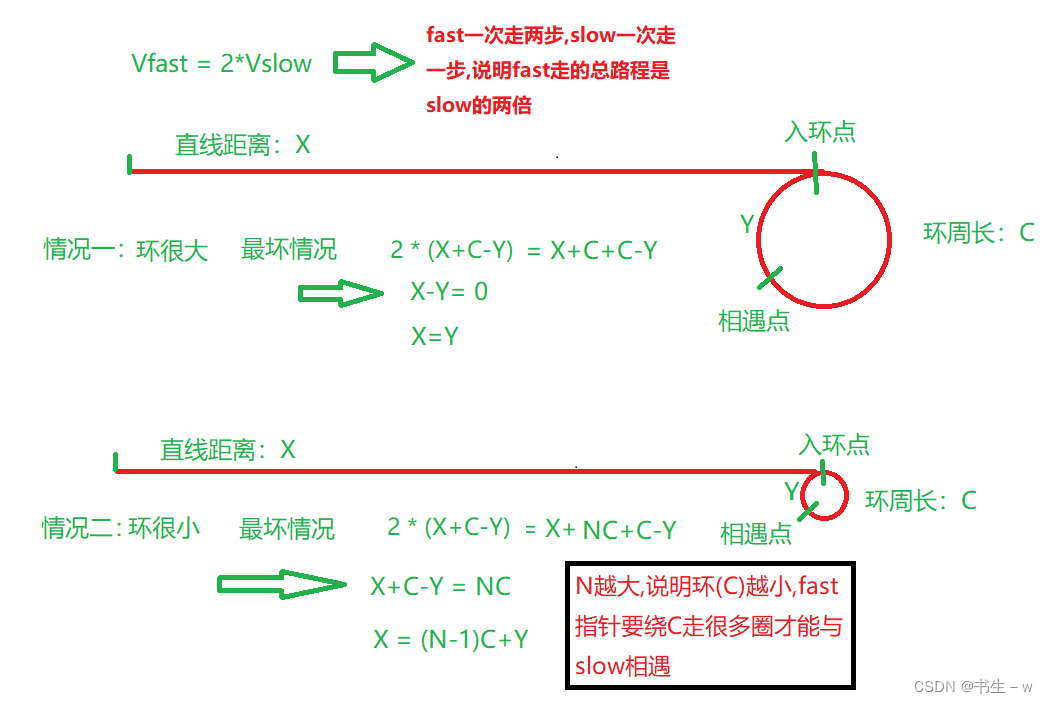
两次遍历链表，每次遍历的时间复杂度都是O(N)，所以总的时间复杂度是O(N) + O(N) = O(N)。

快慢指针解题代码如下

public class Solution {
    public ListNode detectCycle(ListNode head) {
        if(head == null) return null; // 空链表没有环

        //1.先判断链表是否有环(快慢指针)
        ListNode slow = head, fast = head; // 初始化快慢指针
        boolean flag = false; // 标记是否有环
        while(fast != null && fast.next != null) { 
            slow = slow.next; // 慢指针走一步
            fast = fast.next.next; // 快指针走两步
            if(slow == fast) { // 如果快慢指针相遇，说明有环
                flag = true;
                break; // 跳出循环
            }
        }
 
        if(flag) { // 如果有环
            //2.再同时走直到相遇
            slow = head; // 慢指针重新指向头节点
            while(slow != fast) { // 慢指针和快指针同时前进直到它们再次相遇
                slow = slow.next; // 慢指针走一步
                fast = fast.next; // 快指针走一步
            }
            return slow; // 返回入环的第一个节点
        } else {
            return null; // 没有环，返回null
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

# 9. 相交链表

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

图示两个链表在节点 c1 开始相交：

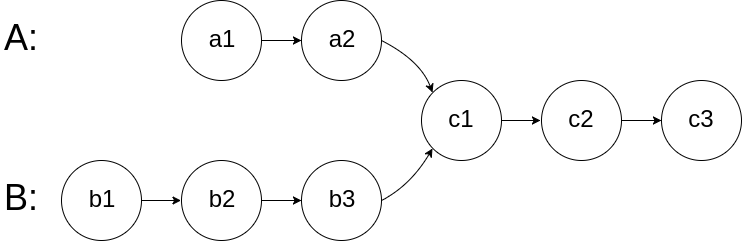
题目数据保证整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

示例 1：

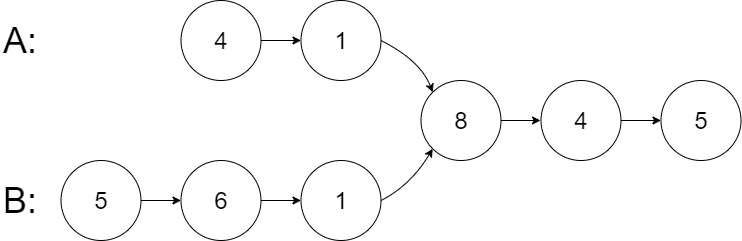
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3

输出：Intersected at '8'

解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。

从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。

在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

— 请注意相交节点的值不为 1，因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说，它们在内存中指向两个不同的位置，而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点，B 中第四个节点) 在内存中指向相同的位置。

提示：

listA 中节点数目为 m
listB 中节点数目为 n
1 <= m, n <= 3 * 104
1 <= Node.val <= 105
0 <= skipA <= m
0 <= skipB <= n
如果 listA 和 listB 没有交点，intersectVal 为 0
如果 listA 和 listB 有交点，intersectVal == listA[skipA] == listB[skipB]

解题思路如下：力扣链接 (opens new window)

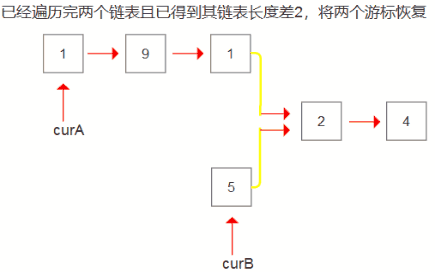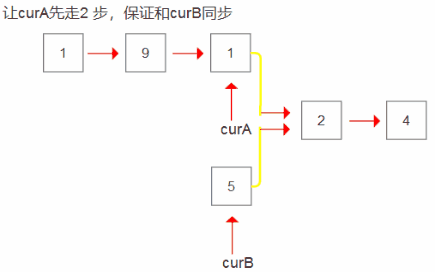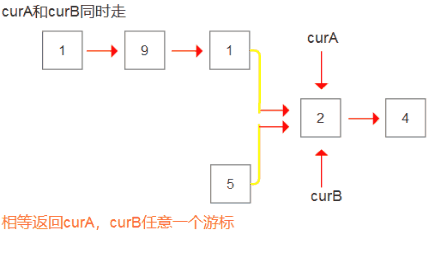
因为两个原始链表不可改动，所以我们使用两个游标结点遍历它们，求出它们的长度。

注意遍历完毕后一定要恢复两个游标结点，方便最后重新进行遍历。

求出它们之间的长度差值，让链表长度较大的那个链表先走差值步。

最后让两个游标结点同时走，直到它们相等，那么它们所在的结点就是两个链表的相交结点，返回它们中任意一个都可以。

时间复杂度O(N+M)，其中N和M分别是两个链表的长度。

双指针解题代码如下

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        // 准备遍历headA和headB的游标节点
        ListNode curA = headA, curB = headB;
 
        // 在相交之前，求出两个链表的长度
        int lenA = 0, lenB = 0;
        while(curA != null) {
            lenA++;
            curA = curA.next; // 遍历链表A
        }
 
        while(curB != null) {
            lenB++;
            curB = curB.next; // 遍历链表B
        }
 
        // 恢复两个游标节点，准备重新遍历
        curA = headA;
        curB = headB;
 
        // 求出两个链表长度的差值
        int len = lenA - lenB;
        if(len < 0) {
            // 确保curA永远指向较长的链表
            curA = headB;
            curB = headA;
            len = -len; // 确保len为非负数
        }
 
        // 让较长的链表先走len步
        while(len != 0) {
            curA = curA.next;
            len--;
        }
 
        // 同时遍历两个链表直到找到相交节点（此时两个链表长度相同）
        while(curA != curB) {
            curA = curA.next;
            curB = curB.next;
        }

        return curA; // 返回相交节点，如果不存在则为null
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

# 10. 反转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

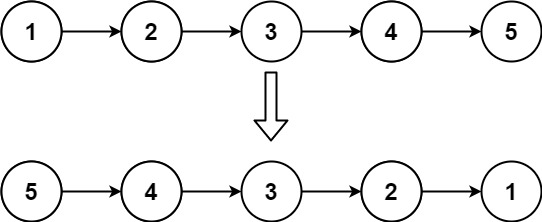
输入：head = [1,2,3,4,5]

输出：[5,4,3,2,1]

示例 2：

输入：head = [1,2]

输出：[2,1]

示例 3：

输入：head = []

输出：[]

提示：

链表中节点的数目范围是 [0, 5000]
-5000 <= Node.val <= 5000

解题思路如下：力扣链接 (opens new window)

# 思路一：头插法

特殊情况处理：如果链表为空或只有一个节点，直接返回原链表头节点。

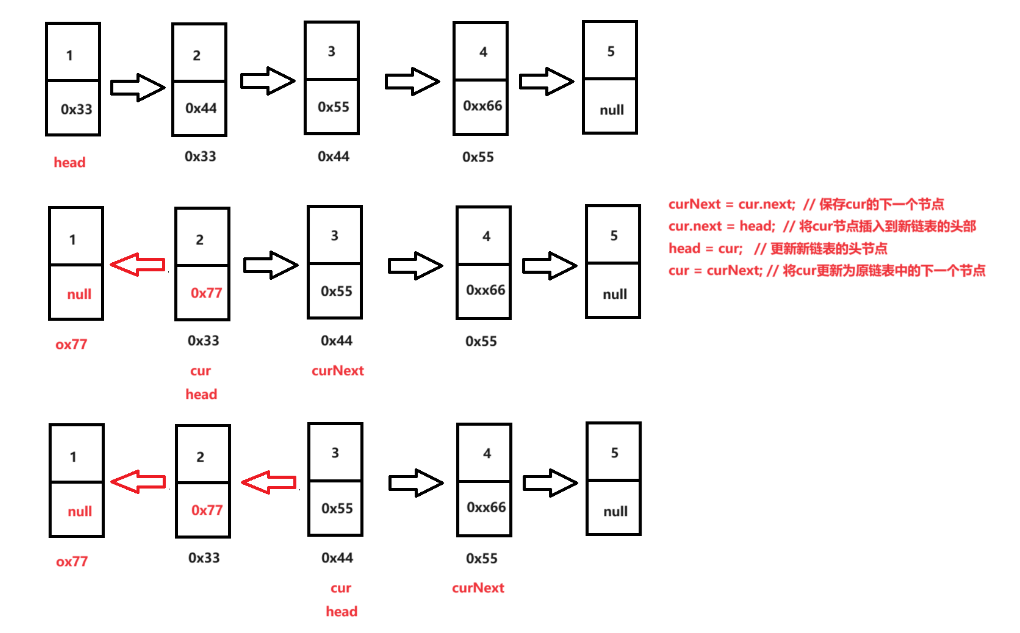
初始化游标：创建一个游标cur指向头节点的下一个节点，因为头节点将成为反转后链表的尾节点。

反转链表：
遍历原链表，每次循环将cur节点进行头插法插入到新链表中。

在插入前，先保存cur的下一个节点为curNext以防丢失剩余链表。

将cur节点插入到新链表头部，然后更新cur为curNext。

当cur为null时，完成所有节点的反转。

返回新链表头节点：在反转过程中，原链表的头节点被转移到了新链表的尾部，新链表的头节点是反转操作完成时的

时间复杂度O(N): 这个算法只需要遍历整个链表一次，其中N是链表的节点数。

class Solution {
    public ListNode reverseList(ListNode head) {
        // 当链表为空或只有一个节点时，无需反转，直接返回
        if(head == null || head.next == null) return head;
 
        // 初始化游标节点cur指向头结点的下一节点
        ListNode cur = head.next;
        head.next = null; // 断开头节点，避免链表成环
 
        // 开始头插法反转链表
        while(cur != null) {
            ListNode curNext = cur.next; // 保存cur的下一个节点，避免链表断裂
            cur.next = head; // 将cur节点插入到新链表的头部
            head = cur; // 更新新链表的头节点
            cur = curNext; // 将cur更新为原链表中的下一个节点
        }
        return head; // 反转完成后，head指向新链表的头节点，返回head
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# 思路二：迭代法

头插法可能更直观易懂，但是在一些复杂的链表操作中，迭代反转更容易集成到其他链表操作中，在迭代过程中，需要三个指针cur（当前节点）、pre（前一节点）和curNext（下一节点）来记录和更新节点。

初始化指针：
pre：指向当前节点cur的前一个节点。初始为null，因为反转后的新链表尾节点的next应该指向null。

cur：当前遍历到的节点，初始时指向头节点head。

curNext：当前节点的下一个节点。这是为了在改变当前节点的next指针前，保存下一个节点的位置，防止链表丢失。

遍历和反转：
在cur不为null的情况下遍历链表，即从头节点开始，一直到链表末尾。

在每一步中，首先记录cur的下一个节点curNext。

然后将cur的next指向pre，实现反转。

最后，移动pre和cur到下一个位置，继续遍历直到cur为null。

返回新头节点：
当遍历完成（cur为null），pre将会指向原链表的末尾节点，这时pre就是新链表的头节点，返回pre。

时间复杂度是O(n)，迭代反转中，只遍历了一次链表，并且每个节点只被访问一次

ListNode reverse(ListNode head) {
    ListNode pre, cur, curNext;
    pre = null; // 前一个节点指针
    cur = head; // 当前节点指针
    curNext = head; // 下一个节点指针
    while (cur != null) { // 遍历链表
        curNext = cur.next; // 记录当前节点的下一个节点
        cur.next = pre; // 反转当前节点的指针
        pre = cur; // 前一个节点指针后移
        cur = nxt; // 当前节点指针后移
    }
    // 返回反转后的头结点
    return pre;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 思路三：递归法

对于递归算法，最重要的就是明确递归函数的定义。具体来说，我们的 reverse 函数定义是这样的：

输入一个节点 head，将「以 head 为起点」的链表反转，并返回反转之后的头结点。

递归的两个条件：

终止条件是当前节点或者下一个节点==null

在函数内部，改变节点的指向，也就是 head 的下一个节点再指向 head 自己完成反转

这里比较难理解的就是head.next.next = head，在递归函数回退的时候，将当前节点下一个节点的指向改成自己完成每个节点反转，每个节点反转成功以后，防止循环链表，所以将当前节点的下一个地址置为null

整个递归过程的时间复杂度为所有递归层次的时间之和，即 O(n)

class Solution {
	public ListNode reverseList(ListNode head) {
		// 递归终止条件：链表为空或只有一个节点，无需反转，直接返回
		if(head==null || head.next==null) {
			return head;
		}
		// 递归反转子链表
		ListNode cur = reverseList(head.next);
		//这里请配合动画演示理解
		//如果链表是 1->2->3->4->5，那么此时的cur就是5
		//而head是4，head的下一个是5，下下一个是空
		//所以head.next.next 就是5->4
		head.next.next = head;
		//防止链表循环，需要将head.next设置为空
		head.next = null;
		//每层递归函数都返回cur，也就是最后一个节点
		return cur;
	}
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# 11. 反转链表||

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。

示例 1：

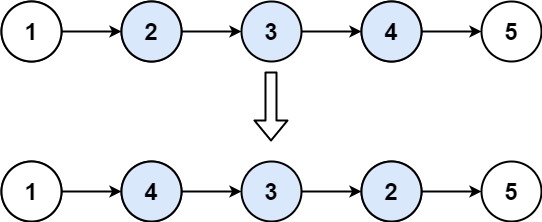
输入：head = [1,2,3,4,5], left = 2, right = 4

输出：[1,4,3,2,5]

示例 2：

输入：head = [5], left = 1, right = 1

输出：[5]

提示：

链表中节点数目为 n
1 <= n <= 500
-500 <= Node.val <= 500
1 <= left <= right <= n

解题思路如下：力扣链接 (opens new window)

初始化指针并找到pre和rightNode:
创建一个虚拟头节点dummy并将head设置为其next节点。这样做是为了简化在链表头部进行反转的操作。

初始化一个指针pre，开始时指向dummy。将此指针向前移动left-1次，使其位于待反转子链表的前一个节点。

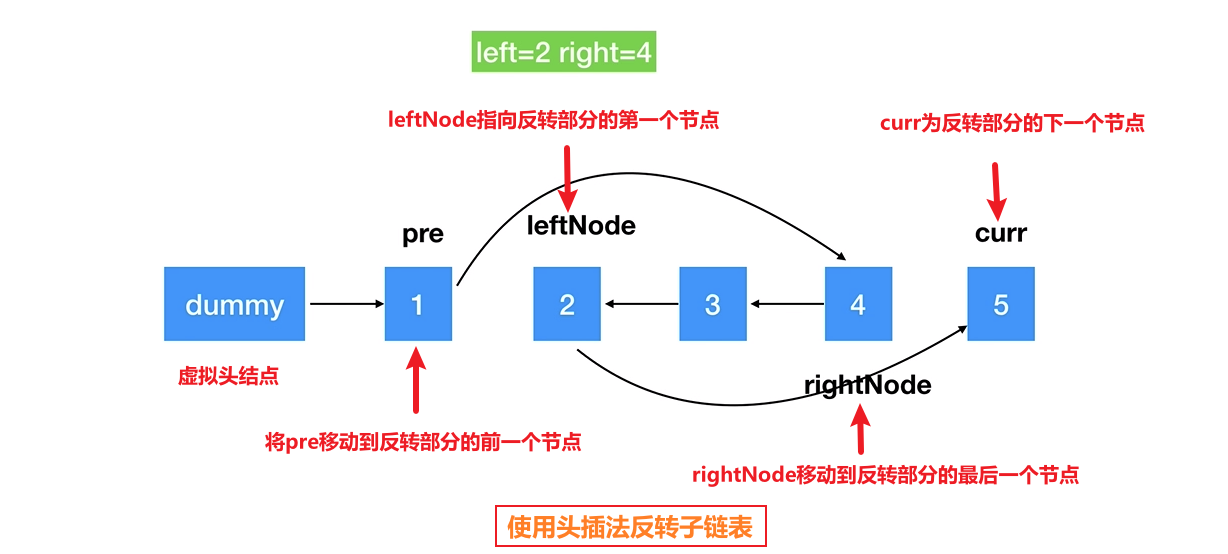
初始化另一个指针rightNode，开始时也指向pre。将此指针向前移动right-left+1次，使其位于待反转子链表的最后一个节点。

断开子链表并反转:
记录rightNode的下一个节点为curr，这是反转部分之后需要连接的链表的头节点。

将pre的next设为null，断开与待反转链表的连接。

同样将rightNode的next设为null，断开子链表。

调用reverseNode函数来反转从leftNode到rightNode的子链表。

重新连接链表:
将pre的next设置为反转后的头节点（现在是rightNode）。

将反转部分的末尾（现在是leftNode）的next设置为curr，以连接未反转的剩余部分。

时间复杂度是O(n)。这里的n是链表的长度，也就是我们需要处理的节点数目

双指针解题代码如下

class Solution {
    public ListNode reverseBetween(ListNode head, int left, int right) {
        ListNode dummy = new ListNode(-1); // 创建虚拟头节点
        dummy.next = head; // 虚拟头结点指向head

        ListNode pre = dummy; // 初始化pre指针

        for(int i = 0; i < left - 1; i++) {
            pre =pre.next; // 将pre移动到反转部分的前一个节点
        }

        ListNode rightNode = pre; 

        for(int i = 0; i < right -left +1; i++) {
            rightNode = rightNode.next; // 将rightNode移动到反转部分的最后一个节点
        }

        ListNode leftNode = pre.next; // leftNode指向反转部分的第一个节点
        ListNode curr = rightNode.next; // curr为rightNode的下一个节点

        // 断开连接
        pre.next = null;
        rightNode.next = null;

        // 反转链表
        reverseNode(leftNode);

        // 重新连接链表
        pre.next = rightNode; // 将反转后的子链表头接到pre后面
        leftNode.next = curr; // 将反转后的子链表尾接到curr前面

        return dummy.next; // 返回整个链表的新头部
    }

    // 使用头插法反转链表
    private void reverseNode(ListNode head) {
        ListNode cur = head.next; // cur指向head的下一个节点
        head.next = null; // 断开head
        while(cur != null) {
            ListNode curNext = cur.next; // 保存cur的下一个节点
            cur.next = head; // 反转
            head = cur; // 移动head到cur
            cur = curNext; // 移动cur到下一个节点
        }
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

# 12. K个一组翻转链表

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

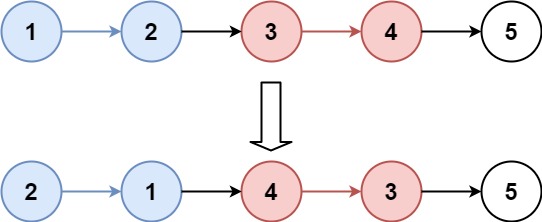
输入：head = [1,2,3,4,5], k = 2

输出：[2,1,4,3,5]

示例 2：

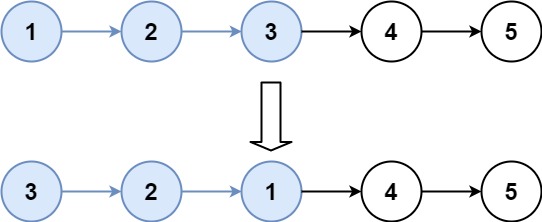
输入：head = [1,2,3,4,5], k = 3

输出：[3,2,1,4,5]

提示：

链表中的节点数目为 n
1 <= k <= n <= 5000
0 <= Node.val <= 1000

解题思路如下：力扣链接 (opens new window)

分组和递归处理：
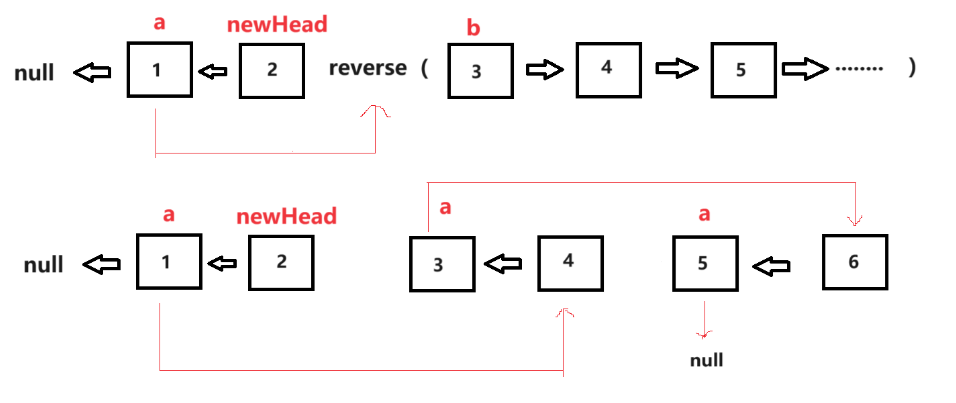
链表被分为多个大小为 k 的小组，每组内部进行翻转。如果链表的长度不是 k 的整数倍，最后剩余的节点保持原顺序。

两个关键指针a和b：
指针 a 表示当前组的开始位置，b 表示当前组的结束位置的下一个节点（即下一组的开始位置）。

反转子链表：
使用一个辅助函数 reverse(a, b) 来实现对链表区间 [a, b) 的反转（左闭右开）。

每一组反转完成以后，指针a都指向当前链表的尾部位置，可以用来连接下一组链表

递归连接：
反转完一组节点后，递归地处理剩余的链表，并将反转后的子链表连接起来。

时间复杂度为 O(n)，其中 n 是链表的长度。每个节点都会被访问一次，以进行翻转操作

递归+双指针解题代码如下

class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        if (head == null) return null;
        // 区间 [a, b) 包含 k 个待反转元素
        ListNode a, b;
        a = b = head;
        // 由于b是从head位置向后走的，所以循环结束以后b在k+1的位置上
        for (int i = 0; i < k; i++) {
            // 不足 k 个，不需要反转
            if (b == null) return head;
            b = b.next;
        }
        // 反转前 k 个元素
        ListNode newHead = reverse(a, b);
        // 每一组k个元素反转成功以后，通过尾指针a去连接下一组链表
        a.next = reverseKGroup(b, k);
        return newHead;
    }

    /* 通过迭代法反转链表区间 [a, b) 的元素，注意是左闭右开 */
    ListNode reverse(ListNode a, ListNode b) {
        ListNode pre, cur, curNext;
        pre = null;
        cur = a;
        curNext = a;
        // while 终止的条件改一下就行了
        while (cur != b) {
            curNext = cur.next;
            cur.next = pre;
            pre = cur;
            cur = curNext;
        }
        // 返回反转后的头结点
        return pre;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

# 13. 回文链表

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

示例 1：

输入：head = [1,2,2,1]

输出：true

示例 2：

输入：head = [1,2]

输出：false

提示：

链表中节点数目在范围[1, 105] 内
0 <= Node.val <= 9

解题思路如下：力扣链接 (opens new window)

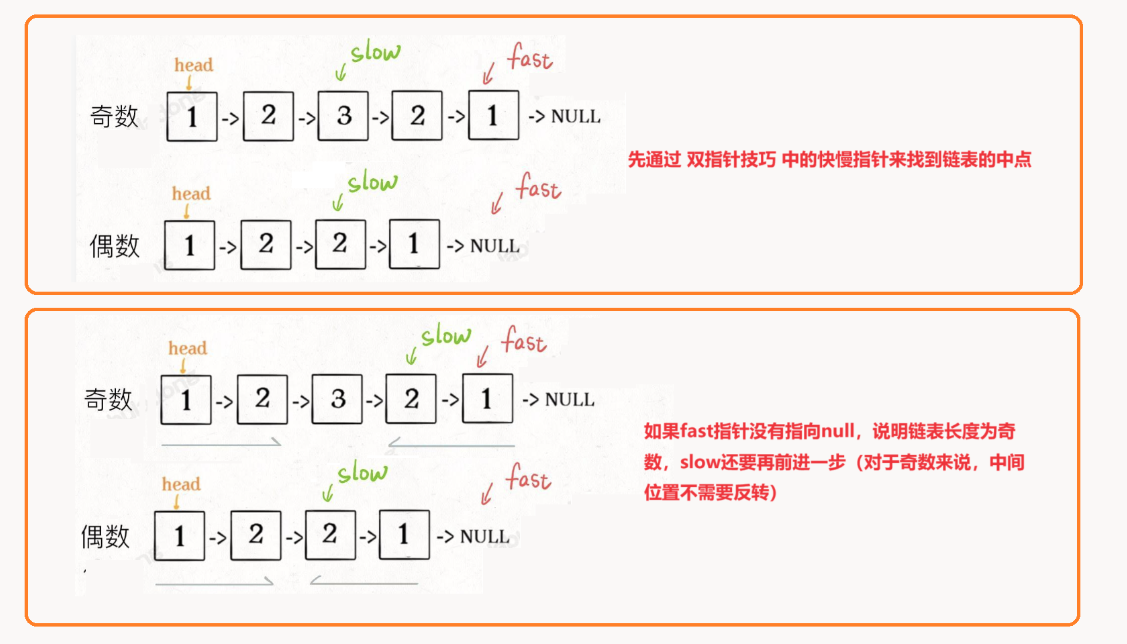
快慢指针定位中点：
使用快慢指针技巧来找到链表的中间节点。快指针一次走两步，慢指针一次走一步，当快指针走到链表末尾时，慢指针恰好在链表的中间。

反转后半部分链表：
从慢指针开始，反转后半部分链表。反转后，我们将得到链表的前半部分和反转后的后半部分，便于接下来的比较操作。

前后半部分比较：
对比链表的前半部分和反转后的后半部分。如果所有元素都相同，则链表是回文的；否则，不是。

时间复杂度是O(n)，尽管有多个步骤，但每个步骤中链表的节点都被线性地访问一次

双指针解题代码如下

boolean isPalindrome(ListNode head) {
    ListNode slow, fast;
    slow = fast = head;
    // 使用快慢指针找到链表的中点
    while (fast != null && fast.next != null) {
        slow = slow.next;
        fast = fast.next.next;
    }
    
    // 如果链表长度为奇数，跳过中间节点
    if (fast != null)
        slow = slow.next;
    
    // 反转后半部分链表
    ListNode left = head;
    ListNode right = reverse(slow);
    
    // 比较前后半部分
    while (right != null) {
        if (left.val != right.val)
            return false; // 值不相等，非回文链表
        left = left.next;
        right = right.next;
    }
    
    return true; // 所有值都相等，是回文链表
}

// 使用迭代法反转链表
ListNode reverse(ListNode head) {
    ListNode pre = null, cur = head;
    while (cur != null) {
        ListNode curNext = cur.next;
        cur.next = pre; // 反转指针
        pre = cur; // 更新pre为当前节点
        cur = curNext; // 移动cur到下一个节点
    }
    return pre; // 返回反转后的头节点
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

# 14. 移除链表元素

给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回 新的头节点 。

示例 1：

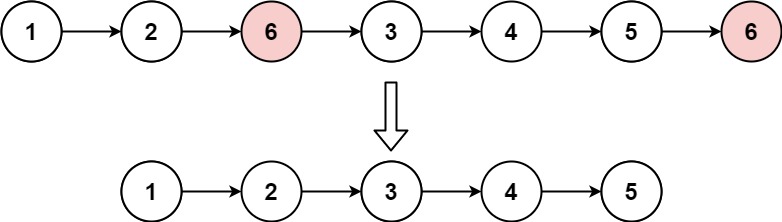
输入：head = [1,2,6,3,4,5,6], val = 6

输出：[1,2,3,4,5]

示例 2：

输入：head = [], val = 1

输出：[]

示例 3：

输入：head = [7,7,7,7], val = 7 输出：[]

提示：

列表中的节点数目在范围 [0, 104] 内
1 <= Node.val <= 50
0 <= val <= 50

解题思路如下：力扣链接 (opens new window)

创建虚拟头结点(dummy)并连接到链表头部：为了方便处理删除头节点的情况，我们先创建一个值为任意值的新节点dummy，将其next指针指向head。这样，即便我们删除了头节点，也能通过dummy.next获得新的头节点。

初始化两个指针：一个当前指针cur指向真正的头节点head，一个前置指针pre指向dummy。这两个指针会帮助我们遍历整个链表并删除目标节点。

遍历链表：遍历整个链表，直到cur指针为空。

删除操作：在遍历过程中，当cur指向的节点值等于val时，我们需要删除该节点。具体操作是将pre的next指向cur的next，即跳过了当前cur所指向的节点。然后将cur后移一位（cur=cur.next）继续检查后续节点。

不删除操作：如果cur指向的节点值不等于val，我们不需要删除节点，只需将pre和cur同时后移一位，继续检查下一个节点。

返回结果：遍历结束后，所有值为val的节点都已被删除。返回dummy.next即可，因为dummy.next指向了新链表的头节点。

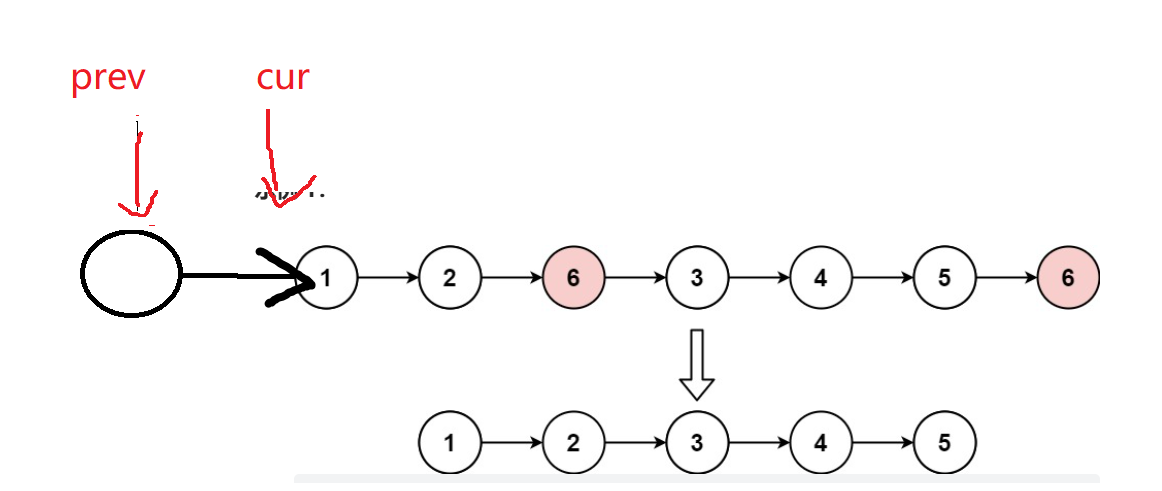
时间复杂度是O(n)，其中n是链表中的节点数量

双指针解题代码如下

class Solution {
    public ListNode removeElements(ListNode head, int val) {
        ListNode dummy = new ListNode(-1); // 创建虚拟头结点
        dummy.next = head; // 连接虚拟头结点到原链表头部
	ListNode pre = dummy; // 前置指针初始化为dummy
        ListNode cur = head; // 当前指针初始化为head    

        while(cur != null) { // 遍历链表
            if(cur.val == val) { // 当前节点需要删除
                pre.next = cur.next; // 前置指针跳过当前节点
                cur = cur.next; // 当前指针后移
            }else { // 当前节点保留
                pre = cur; // 前置指针后移
                cur = cur.next; // 当前指针后移
            }
        }
        return dummy.next; // 返回新链表的头节点
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# 15. 两两交换链表中的节点

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：

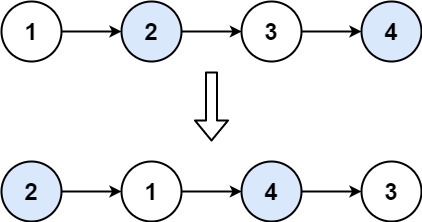
输入：head = [1,2,3,4]

输出：[2,1,4,3]

示例 2：

输入：head = []

输出：[]

示例 3：

输入：head = [1]

输出：[1]

提示：

链表中节点的数目在范围 [0, 100] 内
0 <= Node.val <= 100

解题思路如下：力扣链接 (opens new window)

创建虚拟节点：创建一个虚拟头节点dummy，这是为了方便处理在头部交换节点时的边界条件。将dummy.next指向head。

初始化指针：创建一个cur指针，用于遍历链表，初始时指向dummy。

遍历并交换：进行遍历，每次都要检查cur.next和cur.next.next是否存在，因为我们要交换的是两个节点。只有当这两个节点都不为空时，才能进行交换。

节点交换：按照以下步骤交换节点：
a指向当前节点的下一个节点（cur.next），即第一个要交换的节点。

b指向要交换节点的下一个节点的下一个节点（cur.next.next.next），即第二个要交换的节点的后一个节点，这是为了在交换后能正确连接后续的节点。

让cur.next指向第二个要交换的节点（cur.next.next）。

更新cur.next.next为第一个节点a，此时两个节点已经交换。

更新cur.next.next.next为b，即将原来的第二个节点的后续节点接回链表。

移动cur指针到下一对需要交换的节点的前一个节点，即cur.next.next。

返回结果：最终返回dummy.next，因为dummy指向了整个链表的头部。

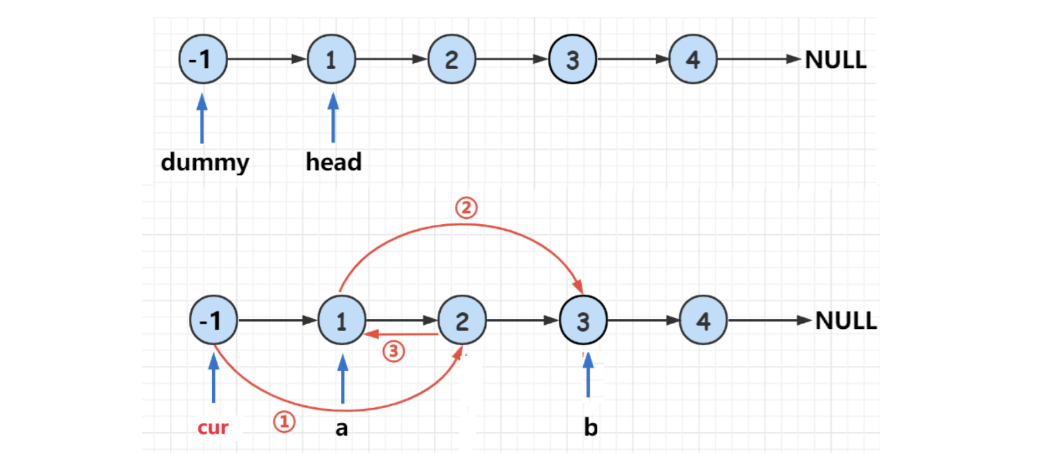
时间复杂度O(N)，其中N是链表的长度。这是因为我们需要遍历整个链表一次，每次交换操作是常数级别的。

双指针解题代码如下

class Solution {
    public ListNode swapPairs(ListNode head) {
        ListNode dummy = new ListNode(-1);  // 创建虚拟头节点
        dummy.next = head;                 // 将虚拟头节点连接到链表头部
        ListNode cur = dummy;              // 初始化cur指针

        // 当存在两个可交换节点时执行
        while(cur.next != null && cur.next.next != null) {
            ListNode a = cur.next;           // a指向第一个交换节点
            ListNode b = cur.next.next.next; // b指向第二个交换节点的后一个节点

            cur.next = cur.next.next;        // 第二个交换节点移到前面
            cur.next.next = a;               // 第一个交换节点移到第二个节点后面
            cur.next.next.next = b;          // 连接后续未处理的节点

            cur = cur.next.next;             // cur移动到下一对待交换节点的前一个节点
        }

        return dummy.next;  // 返回新链表的头节点
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

编辑此页

上次更新: 2025/01/02, 01:21:04

← 数组系列哈希表系列→