• 1. 用栈实现队列
• 2. 用队列实现栈
  • 思路一：使用两个队列实现
  • 思路二：使用一个队列实现
• 3. 有效的括号
• 4. 删除字符串中的所有相邻重复项
  • 思路一：栈
  • 思路二：双指针
• 5. 逆波兰表达式求值
• 6. 滑动窗口最大值
• 7. 前K个高频元素

1. 用栈实现队列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

实现 MyQueue 类：

• void push(int x) 将元素 x 推到队列的末尾
• int pop() 从队列的开头移除并返回元素
• int peek() 返回队列开头的元素
• boolean empty() 如果队列为空，返回 true ；否则，返回 false

说明：

• 你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
• 你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

示例 1：

输入：

["MyQueue", "push", "push", "peek", "pop", "empty"]

[[], [1], [2], [], [], []]

输出：

[null, null, null, 1, 1, false]

解释：

MyQueue myQueue = new MyQueue();

myQueue.push(1); // queue is: [1]

myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)

myQueue.peek(); // return 1

myQueue.pop(); // return 1, queue is [2]

myQueue.empty(); // return false

提示：

• 1 <= x <= 9
• 最多调用 100 次 push、pop、peek 和 empty
• 假设所有操作都是有效的 （例如，一个空的队列不会调用 pop 或者 peek 操作）

解题思路如下：力扣链接 (opens new window)

我们使用两个栈 s1, s2 就能实现一个队列的功能，栈 s1 用于加入队尾操作，栈 s2 用于从队头出队操作。

当调用 push 让元素入队时，只要把元素压入 s1 即可：

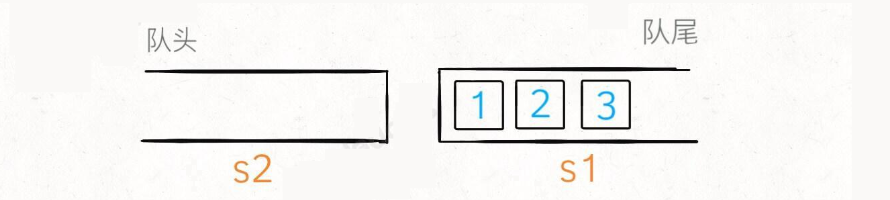
使用 peek 或 pop 操作队头的元素时，若 s2 为空，可以把 s1 的所有元素取出再添加进 s2，这时候 s2 中元素就是先进先出顺序了：

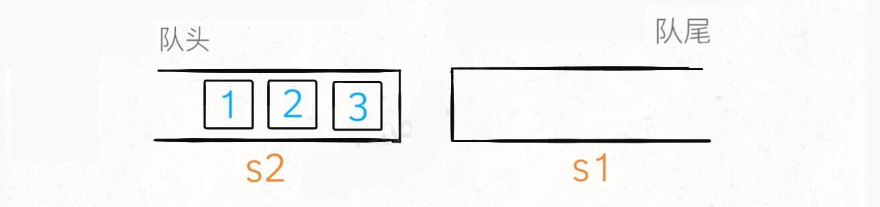
使用两个栈实现代码如下

class MyQueue {
    private Stack<Integer> s1, s2;

    // 构造函数，初始化两个栈
    public MyQueue() {
        s1 = new Stack<>(); // 队尾栈
        s2 = new Stack<>(); // 队头栈
    }

    /**
     * 添加元素到队尾
     * 元素先进入 s1，s1 作为输入栈
     */
    public void push(int x) {
        s1.push(x);
    }

    /**
     * 删除队头的元素并返回
     * 如果 s2 为空，则需要先将 s1 中的元素倒入 s2，实现先入先出
     * 之后从 s2 弹出元素
     */
    public int pop() {
        // 调用 peek 方法来确保 s2 非空，这样才能弹出队头元素
        peek();
        return s2.pop();
    }

    /**
     * 返回队头元素
     * 如果 s2 为空，则先将 s1 中的元素倒入 s2
     * 返回 s2 的栈顶元素，即队头元素
     */
    public int peek() {
        // 如果队列为空，返回 -1
        if (empty()) {
            return -1;
        }
        // 如果 s2 为空，将 s1 的所有元素倒入 s2
        if (s2.isEmpty()) {
            while (!s1.isEmpty()) {
                s2.push(s1.pop());
            }
        }
        // 返回 s2 的栈顶元素
        return s2.peek();
    }

    /**
     * 判断队列是否为空
     * 队列为空当且仅当两个栈都为空
     */
    public boolean empty() {
        return s1.isEmpty() && s2.isEmpty();
    }
}

2. 用队列实现栈

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

• void push(int x) 将元素 x 压入栈顶。
• int pop() 移除并返回栈顶元素。
• int top() 返回栈顶元素。
• boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：

• 你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
• 你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例：

输入：

["MyStack", "push", "push", "top", "pop", "empty"]

[[], [1], [2], [], [], []]

输出：

[null, null, null, 2, 2, false]

解释：

MyStack myStack = new MyStack();

myStack.push(1);

myStack.push(2);

myStack.top(); // 返回 2

myStack.pop(); // 返回 2

myStack.empty(); // 返回 False

提示：

• 1 <= x <= 9
• 最多调用100 次 push、pop、top 和 empty
• 每次调用 pop 和 top 都保证栈不为空

解题思路如下：力扣链接 (opens new window)

思路一：使用两个队列实现

• push 操作：由于栈是后进先出的，因此每次加入一个新元素时，需要保证这个元素位于队列的前端。为此，先将 q1 中的所有元素转移到 q2，然后将新元素加入到 q1，再把 q2 中的元素转回 q1。
• pop 和 top 操作：由于新加入的元素总是在 q1 的队头，因此 q1 的队头元素即为栈顶元素。pop 操作将其出队，top 操作则仅返回队头元素但不出队。
• empty 操作：判断 q1 是否为空即可。

class MyStack {
    // q1 作为主要的队列，其元素排列顺序和出栈顺序相同
    Queue<Integer> q1 = new ArrayDeque<>();
    // q2 仅作为临时放置
    Queue<Integer> q2 = new ArrayDeque<>();

    // 构造方法，初始化两个队列
    public MyStack() {

    }

    /**
     * 将元素 x 压入栈顶
     */
    public void push(int x) {
        // 先将 q1 中的元素依次出队并加入到 q2
        while (!q1.isEmpty()) {
            q2.add(q1.poll());
        }
        // 将新元素 x 加入到 q1
        q1.add(x);
        // 再将 q2 中的元素依次出队并加入到 q1
        // 这样做的目的是保证最新加入的元素始终在 q1 的队头，模拟栈的后进先出特性
        while (!q2.isEmpty()) {
            q1.add(q2.poll());
        }
    }

    /**
     * 移除并返回栈顶元素
     */
    public int pop() {
        // q1 的队头元素即为栈顶元素，出队并返回
        return q1.poll();
    }

    /**
     * 返回栈顶元素
     */
    public int top() {
        // q1 的队头元素即为栈顶元素，返回但不出队
        return q1.peek();
    }

    /**
     * 判断栈是否为空
     */
    public boolean empty() {
        // 栈为空当且仅当 q1 为空
        return q1.isEmpty();
    }
}

思路二：使用一个队列实现

这个解法是使用单个队列模拟栈的一种方法。与栈的后进先出（LIFO）不同，队列通常是先进先出（FIFO）。为了模拟栈的行为，每次新元素被加入时，队列中的元素顺序会被重新排列，确保新加入的元素位于队列的开头。

class MyStack {
    Queue<Integer> queue;

    public MyStack() {
        queue = new LinkedList<>();
    }

    /**
     * 模拟压栈操作
     * 将新元素加入队列，然后将除了新加入元素外的所有元素出队并重新入队
     * 这样可以保证新加入的元素始终在队列的开头
     */
    public void push(int x) {
        queue.offer(x);
        int size = queue.size();
        // 将队列中的元素重新排列，确保最新添加的元素在队首
        while (size > 1) {
            queue.offer(queue.poll());
            size--;
        }
    }

    /**
     * 模拟出栈操作
     * 由于新元素总是位于队列的开头，所以直接出队即可
     */
    public int pop() {
        return queue.poll();
    }

    /**
     * 获取栈顶元素
     * 直接返回队列的队首元素
     */
    public int top() {
        return queue.peek();
    }

    /**
     * 判断栈是否为空
     * 检查队列是否为空
     */
    public boolean empty() {
        return queue.isEmpty();
    }
}

3. 有效的括号

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

1. 左括号必须用相同类型的右括号闭合。
2. 左括号必须以正确的顺序闭合。
3. 每个右括号都有一个对应的相同类型的左括号。

示例 1：

输入：s = "()" 输出：true

示例 2：

输入：s = "()[]{}" 输出：true

示例 3：

输入：s = "(]" 输出：false

提示：

• 1 <= s.length <= 104
• s 仅由括号 '()[]{}' 组成

解题思路如下：力扣链接 (opens new window)

题意其实就像我们在写代码的过程中，要求括号的顺序是一样的，有左括号，相应的位置必须要有右括号。

首先要弄清楚，字符串里的括号不匹配有几种情况。

1. 第一种情况，字符串里左方向的括号多余了 ，所以不匹配。
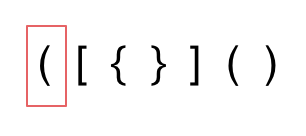
2. 第二种情况，括号没有多余，但是 括号的类型没有匹配上。
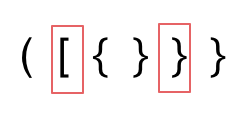
3. 第三种情况，字符串里右方向的括号多余了，所以不匹配。

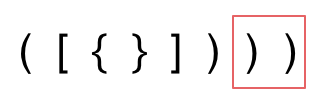
我们的代码只要覆盖了这三种不匹配的情况，就不会出问题，下面看具体解题思路：

1. 创建一个栈来存储期待出现的右括号序列，以确保括号正确配对

2. 遍历给定字符串，如果遇到一个左括号，我们不将这个左括号本身入栈，而是将与之对应的右括号入栈。

3. 后续如果遇到一个右括号，我们检查它是否与栈顶元素（即最近一个未匹配的左括号的对应右括号）相同。

   • 如果相同，则说明找到了一个匹配的括号对，将栈顶元素弹出。

   • 如果不同或栈为空，则说明括号序列无效，可以直接返回 false。

这种方法的优点是在进行匹配检查时不需要对每个右括号进行分类判断（即不需要检查是 ')' 还是 '}' 或 ']），只需要看它是否与栈顶元素相同即可。

• 时间复杂度为 O(n)，其中 n 是字符串 s 的长度，因为需要遍历一次字符串

栈实现代码如下

class Solution {
    public boolean isValid(String s) {
        // 使用双端队列作为栈结构
        Deque<Character> deque = new LinkedList<>();
        char ch;
        // 遍历字符串中的每一个字符
        for (int i = 0; i < s.length(); i++) {
            ch = s.charAt(i);
            // 如果字符是左括号，将对应的右括号压入栈中
            if (ch == '(') {
                deque.push(')');
            } else if (ch == '{') {
                deque.push('}');
            } else if (ch == '[') {
                deque.push(']');
            } else {
                // 如果字符是右括号，检查栈是否为空或栈顶元素是否与之匹配
                if (deque.isEmpty() || deque.peek() != ch) {
                    return false; // 不匹配或栈为空则返回 false
                } else {
                    deque.pop(); // 匹配则弹出栈顶元素
                }
            }
        }
        // 遍历结束后，检查栈是否为空，为空则说明括号完全匹配
        return deque.isEmpty();
    }
}

4. 删除字符串中的所有相邻重复项

给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 S 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

示例：

输入："abbaca"

输出："ca"

解释：

例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。

提示：

1. 1 <= S.length <= 20000
2. S 仅由小写英文字母组成。

解题思路如下：力扣链接 (opens new window)

思路一：栈

在这个问题中，我们使用栈（这里使用 ArrayDeque 实现）来处理重复项删除操作。基本思想是遍历字符串 S，每次检查栈顶元素是否与当前字符相同。如果相同，就从栈中弹出（删除）该元素；如果不同，就将当前字符压入栈中。这样，栈中的元素总是不重复的。最后，将栈中剩余的元素构造成字符串，这就是删除所有重复项后的结果。

• 时间复杂度是 O(N)，其中 N 是字符串 S 的长度，因为每个字符最多被压入和弹出栈一次。
• 空间复杂度也是 O(N)，最坏情况下栈中可能包含整个字符串的所有字符。

class Solution {
    public String removeDuplicates(String s) {
        // 使用 ArrayDeque 作为栈结构，相比 LinkedList 有更好的性能
        ArrayDeque<Character> deque = new ArrayDeque<>();

        // 遍历字符串 s
        for (int i = 0; i < s.length(); i++) {
            char ch = s.charAt(i);
            // 如果栈为空或栈顶元素不等于当前字符，则将字符压入栈
            if (deque.isEmpty() || deque.peek() != ch) {
                deque.push(ch);
            } else {
                // 否则，栈顶元素与当前字符相同，弹出栈顶元素（删除重复项）
                deque.pop();
            }
        }

        // 构建结果字符串
        String str = "";
        // 从栈中弹出所有元素，得到最终字符串（反序拼接）
        while (!deque.isEmpty()) {
            str = deque.pop() + str;
        }

        // 返回处理后的字符串
        return str;
    }
}

思路二：双指针

• 核心思想是利用双指针进行原地修改，通过左指针记录处理后字符串的末尾，右指针遍历原字符串。
• 当遇到重复字符时，左指针后退以删除重复字符；否则，左指针前进以保留当前字符。
• 通过这种方式，能够有效地移除字符串中的重复字符，实现原地修改。

• 时间复杂度为 O(N)，其中 N 是字符串的长度。

class Solution {
    public String removeDuplicates(String S) {
        int left = 0; // 左指针，表示处理后字符串的长度
        int right = 0; // 右指针，遍历原字符串
        int length = S.length(); // 字符串长度
        char[] chars = S.toCharArray(); // 字符串转化为字符数组

        while (right < length) {
            chars[left] = chars[right]; // 把右指针的字符赋值给左指针位置
            // 如果左指针前一个字符与当前字符相同，则后退两步删除重复字符
            if (left > 0 && chars[left - 1] == chars[left])
                left -= 2;
            right++; // 移动右指针
            left++; // 移动左指针
        }
        return new String(chars, 0, left); // 返回处理后的字符串
    }
}

5. 逆波兰表达式求值

给你一个字符串数组 tokens ，表示一个根据 逆波兰表示法 (opens new window) 表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

注意：

• 有效的算符为 '+'、'-'、'*' 和 '/' 。
• 每个操作数（运算对象）都可以是一个整数或者另一个表达式。
• 两个整数之间的除法总是 向零截断 。
• 表达式中不含除零运算。
• 输入是一个根据逆波兰表示法表示的算术表达式。
• 答案及所有中间计算结果可以用 32 位 整数表示。

示例 1：

输入：tokens = ["2","1","+","3","*"]

输出：9

解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

输入：tokens = ["4","13","5","/","+"]

输出：6

解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：

输入：tokens = ["10","6","9","3","+","-11","","/","","17","+","5","+"]

输出：22

解释：该算式转化为常见的中缀算术表达式为：

((10 * (6 / ((9 + 3) * -11))) + 17) + 5

= ((10 * (6 / (12 * -11))) + 17) + 5

= ((10 * (6 / -132)) + 17) + 5

= ((10 * 0) + 17) + 5

= (0 + 17) + 5

= 17 + 5

= 22

提示：

• 1 <= tokens.length <= 104
• tokens[i] 是一个算符（"+"、"-"、"*" 或 "/"），或是在范围 [-200, 200] 内的一个整数

解题思路如下：力扣链接 (opens new window)

在讲解这个题之前给大家普及一点知识，我们平时的算术表达式中，运算符总是出现在两个操作数之间，例如 5 * (7 - 2 * 3) + 8 / 2 ,这种形式叫做中缀表达式，而我们的逆波兰表达式又叫后缀表达式，那什么是后缀表达式呢???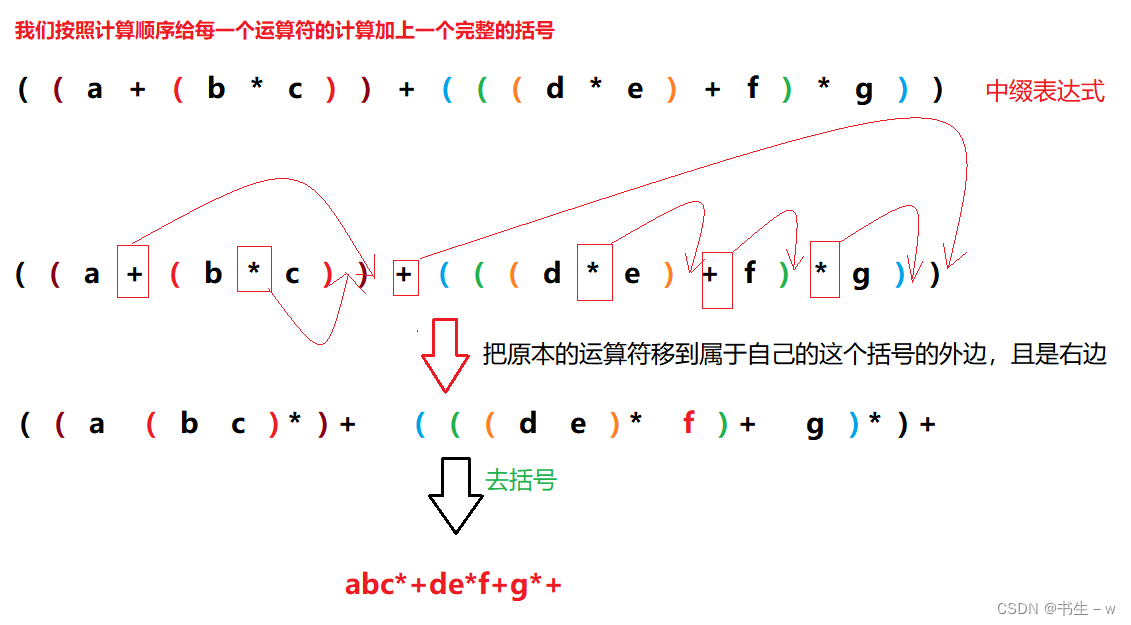

我们把中缀表达式的运算符移动到自己所在的括号的右括号的右边，然后再去括号，这就是逆波兰表达式，那这个东西该怎么计算呢？？？

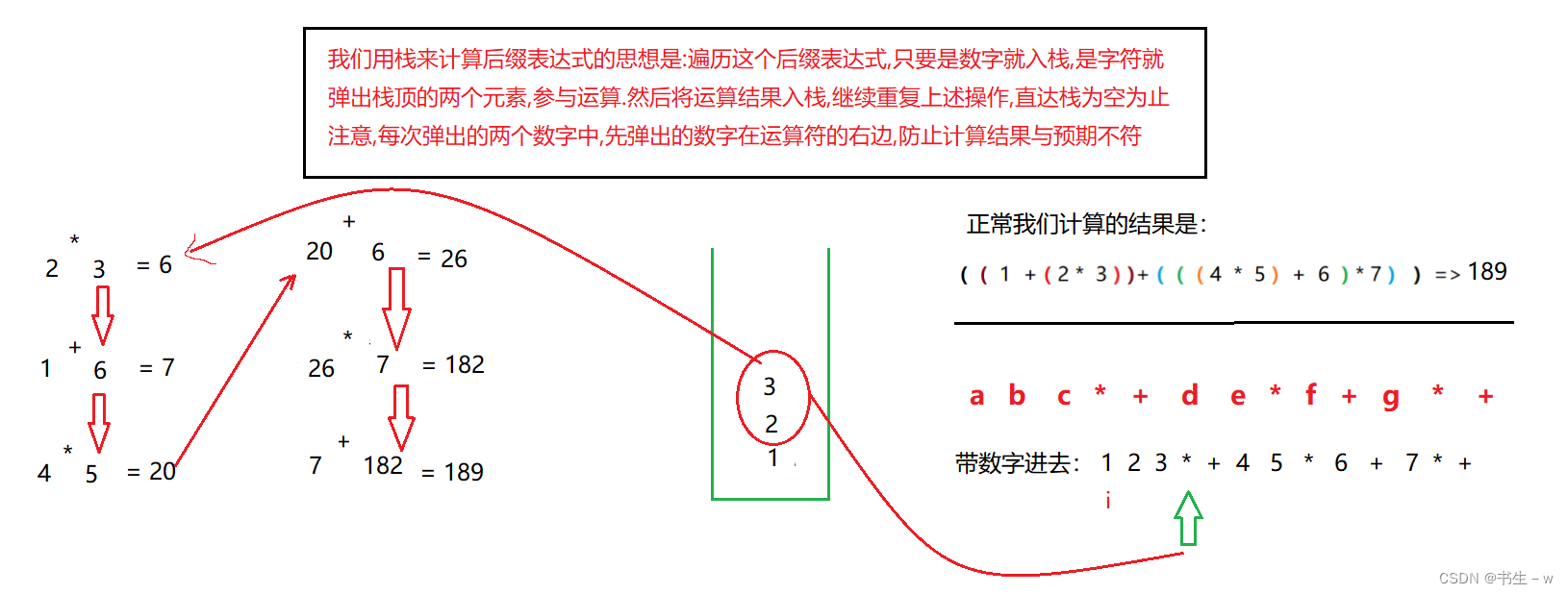
具体解题思路如下：

1. 初始化栈：用于存储操作数的栈 stack。
2. 遍历表达式：遍历给定的字符串数组 tokens，对每个元素进行处理。
3. 操作数入栈：如果当前元素是数字，将其转换为整数并压入栈中。
4. 操作符处理：如果当前元素是操作符，从栈中弹出两个元素作为操作数。这里要注意操作数的顺序，第二个弹出的元素是第一个操作数，第一个弹出的是第二个操作数。
5. 计算结果：根据操作符执行相应的计算，并将结果压回栈中。
6. 返回结果：表达式遍历完成后，栈顶元素即为最终的计算结果。

栈解题代码如下

class Solution {
    public int evalRPN(String[] tokens) {
        Deque<Integer> stack = new ArrayDeque<>(); // 存储操作数的栈

        for (String token : tokens) {
            if (!isOperator(token)) {
                // 如果是数字，转换成整数并压入栈
                stack.push(Integer.parseInt(token));
            } else {
                // 如果是操作符，弹出两个操作数进行计算
                int num1 = stack.pop(); // 第二个操作数
                int num2 = stack.pop(); // 第一个操作数
                int result = 0; // 计算结果
                switch (token) {
                    case "+":
                        result = num2 + num1;
                        break;
                    case "-":
                        result = num2 - num1;
                        break;
                    case "*":
                        result = num2 * num1;
                        break;
                    case "/":
                        result = num2 / num1; // 注意向零截断的整数除法
                        break;
                }
                // 将计算结果压回栈
                stack.push(result);
            }
        }
        // 返回栈顶元素，即最终的计算结果
        return stack.pop();
    }

    // 判断是否为操作符
    public boolean isOperator(String s) {
        return s.equals("+") || s.equals("-") || s.equals("*") || s.equals("/");
    }
}

6. 滑动窗口最大值

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3

输出：[3,3,5,5,6,7]

解释：

滑动窗口的位置 最大值

[1 3 -1] -3 5 3 6 7 3

1 [3 -1 -3] 5 3 6 7 3

1 3 [-1 -3 5] 3 6 7 5

1 3 -1 [-3 5 3] 6 7 5

1 3 -1 -3 [5 3 6] 7 6

1 3 -1 -3 5 [3 6 7] 7

示例 2：

输入：nums = [1], k = 1

输出：[1]

提示：

• 1 <= nums.length <= 105
• -104 <= nums[i] <= 104
• 1 <= k <= nums.length

解题思路如下：力扣链接 (opens new window)

在解决滑动窗口中的最大值问题时，核心思想是如何快速从窗口中找到最大值。这里使用的“单调队列”是解决这一问题的关键。单调队列是一种特殊的队列结构，它能够保证队列内的元素始终保持单调递减（或递增）的顺序。该队列没有必要维护窗口里的所有元素，只需要维护有可能成为窗口里最大值的元素就可以了，同时保证队列里的元素数值是由大到小的。

1. 定义单调队列：
   • 创建一个名为 MyQueue 的内部类来实现单调队列，用以存储当前窗口的所有元素，并确保队列始终保持单调递减的顺序。队列中的第一个元素始终是当前窗口中的最大值。
2. 单调队列的操作：
   • 入队操作 (push)：当一个新元素准备入队时，从队列尾部开始移除所有小于该新元素的值，然后将新元素添加到队列末尾。这样做确保了队列始终保持单调递减的顺序。
   • 获取最大值 (max)：直接返回队列的第一个元素，即当前窗口的最大值。
   • 出队操作 (pop)：当窗口滑动，即一个元素即将离开窗口时，如果该元素等于队列的第一个元素，表示当前窗口的最大值即将离开，因此需要从队列中移除。如果不等于，那么这个元素不在队列中，因为所有小于窗口最大值的元素都已被之前的入队逻辑移除。
3. 遍历输入数组 nums：
   • 遍历数组 nums，使用单调队列来维护当前窗口内的元素。
   • 对于数组中的每个元素，将其加入单调队列，如果 i 小于 k - 1，即窗口未满时，先前窗口填满至k个大小。
   • 当窗口大小达到 k 时，记录当前窗口的最大值（即单调队列的第一个元素）到结果数组中。
   • 同时，当窗口向右滑动时，调用 pop 方法从单调队列中移除即将离开窗口的元素。
4. 构建结果数组：
   • 使用单调队列中的最大值构建最终的结果数组，该数组包含了每个窗口的最大值。

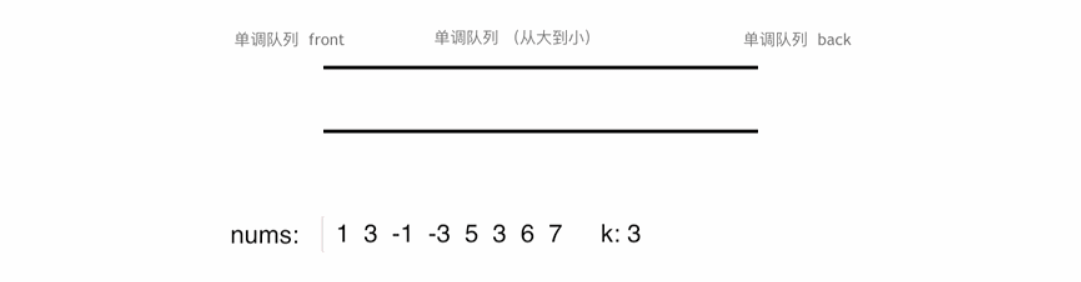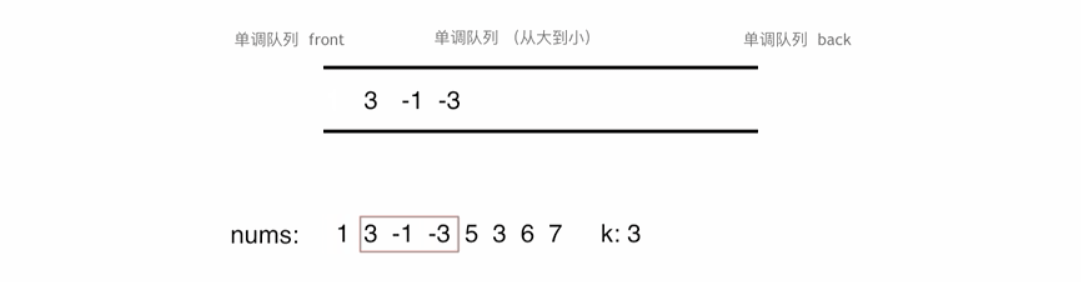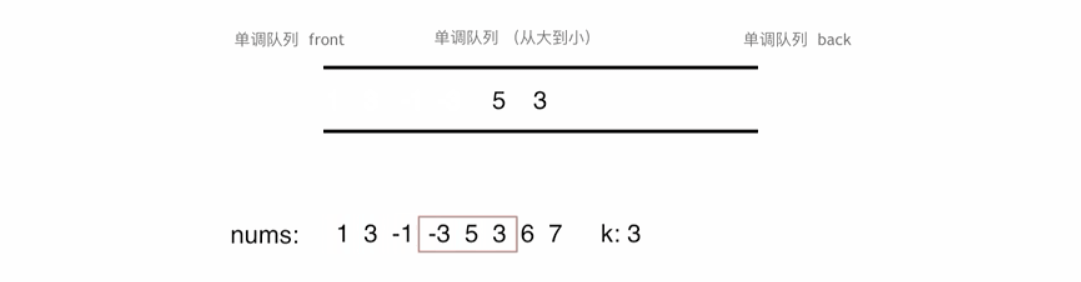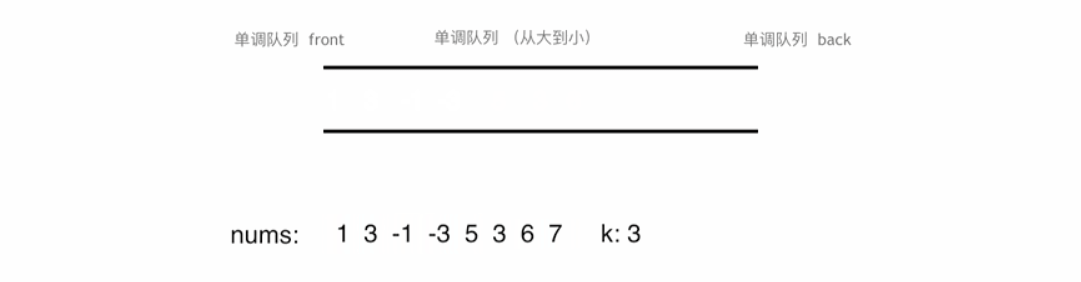
• 时间复杂度也是 O(n)，因为每个元素最多被添加和删除一次。

• 空间复杂度是 O(k)，其中 k 是窗口的大小。

单调栈示例代码如下

class Solution {
    /* 单调队列的实现 */
    class MyQueue{
        Deque<Integer> q = new LinkedList<>();

        // 入队操作
        public void push(int n) {
            // 从队列尾部开始，移除所有小于 n 的元素
            while (!q.isEmpty() && q.getLast() < n) {
                q.removeLast();
            }
            // 将新元素 n 加入队列尾部
            q.addLast(n);
        }

        // 获取队列中的最大值
        public int max() {
            // 返回队列头部元素，即为当前队列中的最大值
            return q.getFirst();
        }

        // 出队操作
        public void pop(int n) {
            // 只有当要移除的元素 n 等于队列头部元素时，才进行移除
            if (n == q.getFirst()) {
                q.removeFirst();
            }
        }
    }

    /* 解题函数的实现 */
    public int[] maxSlidingWindow(int[] nums, int k) {
        MyQueue window = new MyQueue();
        List<Integer> res = new ArrayList<>();

        for (int i = 0; i < nums.length; i++) {
            if (i < k - 1) {
                // 在窗口填满 k - 1 个元素之前，先将元素加入队列
                window.push(nums[i]);
            } else {
                // 窗口已满，继续向前滑动窗口，加入新的元素
                window.push(nums[i]);
                // 记录当前窗口的最大值
                res.add(window.max());
                // 移出窗口最左端的元素
                window.pop(nums[i - k + 1]);
            }
        }

        // 将 List 转换为数组，并返回
        int[] arr = new int[res.size()];
        for (int i = 0; i < res.size(); i++) {
            arr[i] = res.get(i);
        }
        return arr;
    }
}

7. 前K个高频元素

给你一个整数数组 nums 和一个整数 k ，请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。

示例 1:

输入: nums = [1,1,1,2,2,3], k = 2

输出: [1,2]

示例 2:

输入: nums = [1], k = 1

输出: [1]

提示：

• 1 <= nums.length <= 105
• k 的取值范围是 [1, 数组中不相同的元素的个数]
• 题目数据保证答案唯一，换句话说，数组中前 k 个高频元素的集合是唯一的

解题思路如下：力扣链接 (opens new window)

对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决，基本思路如下：

堆是一棵完全二叉树，树中每个结点的值都不小于（或不大于）其左右孩子的值。 如果父亲结点是大于等于左右孩子就是大顶堆，小于等于左右孩子就是小顶堆。

有的同学一想，题目要求前 K 个高频元素，那么果断用大顶堆啊。

那么问题来了，定义一个大小为k的大顶堆，在每次移动更新大顶堆的时候，每次弹出都把最大的元素弹出去了，那么怎么保留下来前K个高频元素呢。

而且使用大顶堆就要把所有元素都进行排序，那能不能只排序k个元素呢？

所以我们要用小顶堆，因为要统计最大前k个元素，只有小顶堆每次将最小的元素弹出，最后小顶堆里积累的才是前k个最大元素。

1. 哈希表统计频率：首先使用一个哈希表 map 来统计每个元素出现的次数。
2. 构建小根堆：然后创建一个小根堆 minHeap，其中堆的大小被限制为 k。小根堆用于存储频率最高的 k 个元素，但是以频率作为比较的依据，这是通过提供一个自定义比较器来实现的。
3. 维护堆的大小：遍历哈希表，将元素添加到堆中。如果堆的大小超过 k，则移除堆顶元素，以确保堆中始终保持频率最高的 k 个元素。
4. 提取结果：最后，将堆中的元素提取出来，存入结果数组 arr 并返回。

• 时间复杂度为 O(N*log k)，其中 N 是数组 nums 的长度，k 是要找出的高频元素的个数。

小顶堆解题代码如下

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        // 使用哈希表统计每个元素出现的频率
        Map<Integer, Integer> map = new HashMap<>();
        for (int num : nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
        }

        // 构建一个小根堆，这个堆用于维护出现频率最高的 k 个元素
        // 使用自定义的比较器，使得堆是按照元素的频率排序的
        PriorityQueue<Integer> minHeap= new PriorityQueue<>((o1, o2) -> (map.get(o1) - map.get(o2)));

        // 遍历频率哈希表，维护一个大小为 k 的小根堆
        for (int num : map.keySet()) {
            if (minHeap.size() < k) {
                // 如果堆的大小小于 k，直接添加
                minHeap.add(num);
            } else if (map.get(num) > map.get(minHeap.peek())) {
                // 如果当前数字的频率大于堆顶元素的频率，则弹出堆顶元素，将当前元素加入堆中
                minHeap.poll();
                minHeap.add(num);
            }
        }

        // 从堆中取出所有元素，存入结果数组
        int[] arr = new int[k];
        for (int i = 0; i < k; ++i) {
            arr[i] = minHeap.poll();
        }
        return arr;
    }
}