一、概念

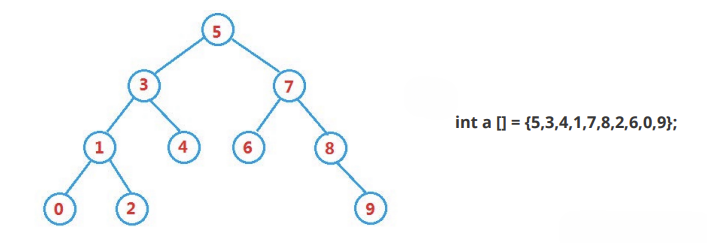
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

1. 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
2. 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
3. 它的左右子树也分别为二叉搜索树

提示：二叉搜索树的中序遍历一定是有序的（从小到大）

​

二、实现一个二叉搜索树

2.1 成员变量

public class BinarySearchTree {
    private TreeNode root; //存放根节点
 
    private static class TreeNode {
        private int val;
        private TreeNode left;
        private TreeNode right;
        private TreeNode(int val) {
            this.val = val;
        }
    }
}

这里跟我们的二叉树成员变量大同小异，主要是去实现插入，查找，删除的逻辑。

2.2 搜索树的查找

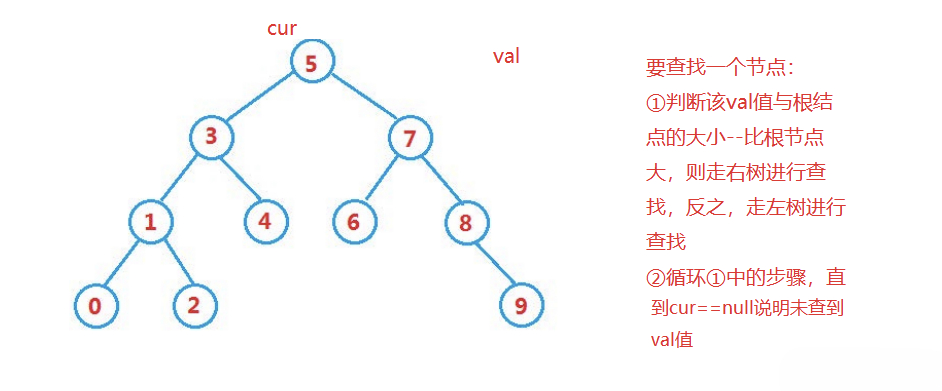
代码如下：

public Node search(int key){
        TreeNode cur=root;
        while(cur!=null){
            if(cur.val<key){
                cur=cur.right;
            }else if(cur.val==key){
                return cur;
            }else{
                cur=cur.left;
            }
        }
        return null;//走到这里，说明上面while没找到，也就是没有这个数据
    }

2.3 操作—插入

1.如果树为空树，即根为null，就可以直接插入。

2.如果树非空树，应按照查找逻辑找到插入位置，插入新节点。

• ​ 通过查找的规则来寻找插入节点，每次插入的节点都为叶子节点！
• ​ 注意相同的key是不可以插入的！

从根节点开始，根据查找的规则用cur进行节点遍历，同时用prev来存储遍历的前一个节点，直到cur == null时，此时prev已经遍历到叶子节点，再进行判断key与该叶子节点的大小关系来决定放在left还是right。

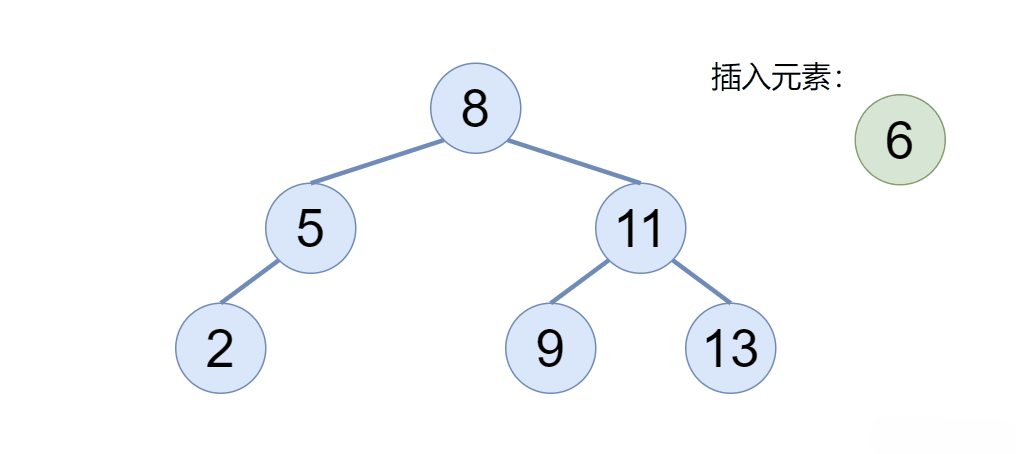
代码如下:

public boolean insert(int key) {
    // 二叉搜索树没有节点的情况
    if (root == null) {
        root = new TreeNode(key);
        return true;
    }
    // 二叉搜索树不为空的情况 -> 找到该节点要插入的位置进行插入
    // 如果已经存在该节点了, 则不用插入 -> 二叉搜索树中不能出现重复值
    TreeNode parent = null; // 记录cur的父节点
    TreeNode cur = root;
    while (cur != null) {
        if (cur.val < key) {
            parent = cur;
            cur = cur.right;
        } else if (cur.val > key) {
            parent = cur;
            cur = cur.left;
        } else {
            return false; // 插入重复的节点
        }
    }
    // 走到这, cur为空了, key 需要插入到 parent 的左节点或右节点中
    TreeNode newNode = new TreeNode(key);
    if (parent.val < key) {
        parent.right = newNode;
    } else {
        parent.left = newNode;
    }
    return true;
}

2.4 搜索树的删除（难点）

解题思路：

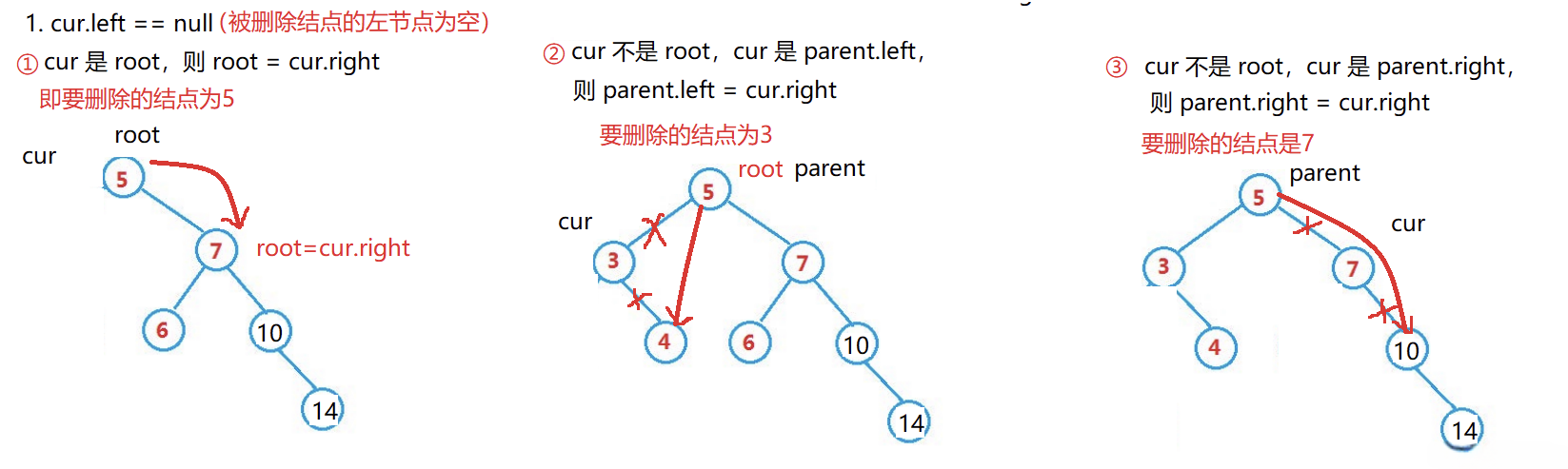
1. cur.left == null

• ①cur 是 root ，则 root = cur.right
• ②cur 不是 root ， cur 是 parent.left ，则 parent.left = cur.right
• ③cur 不是 root， cur 是 parent.right ，则 parent.right = cur.right

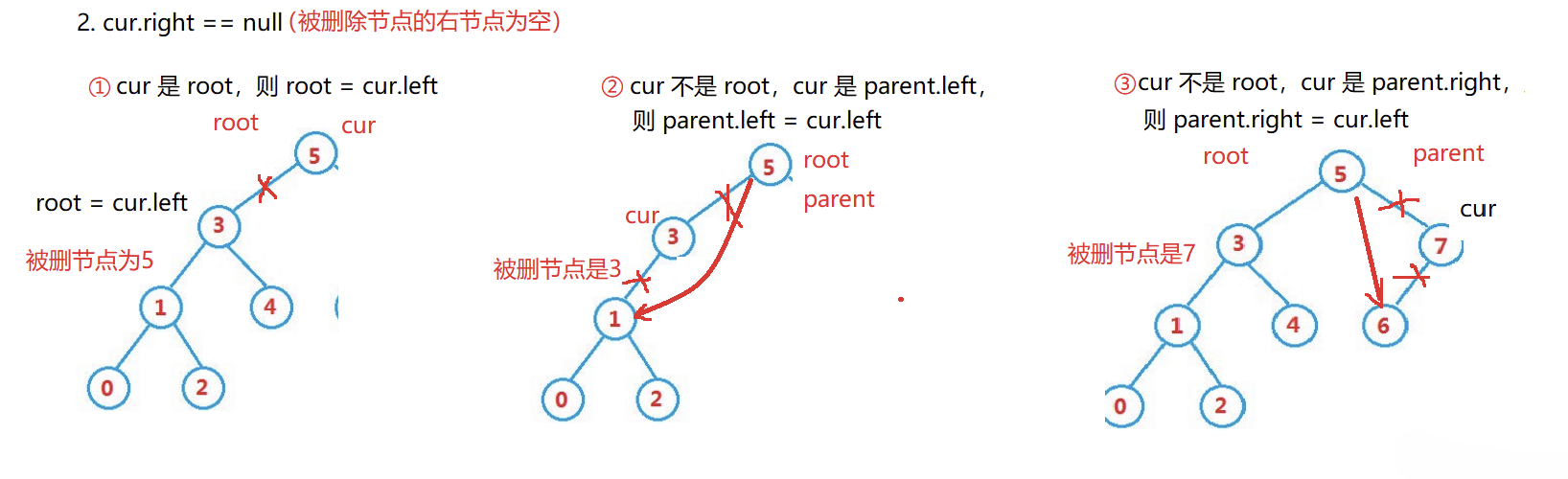
2. cur.right == null

• ①cur 是 root ，则 root = cur.left
• ②cur 不是 root ， cur 是 parent.left ，则 parent.left = cur.left
• ③cur 不是 root ， cur 是 parent.right ，则 parent.right = cur.left

3. cur.left != null && cur.right != null（难点）

思路： 需要使用 替换法 进行删除，即在需删除节点的左子树中找到最大值或者在右子树中找到最小值, 用它的值填补到被删除节点中，然后再来处理这个结点的删除问题

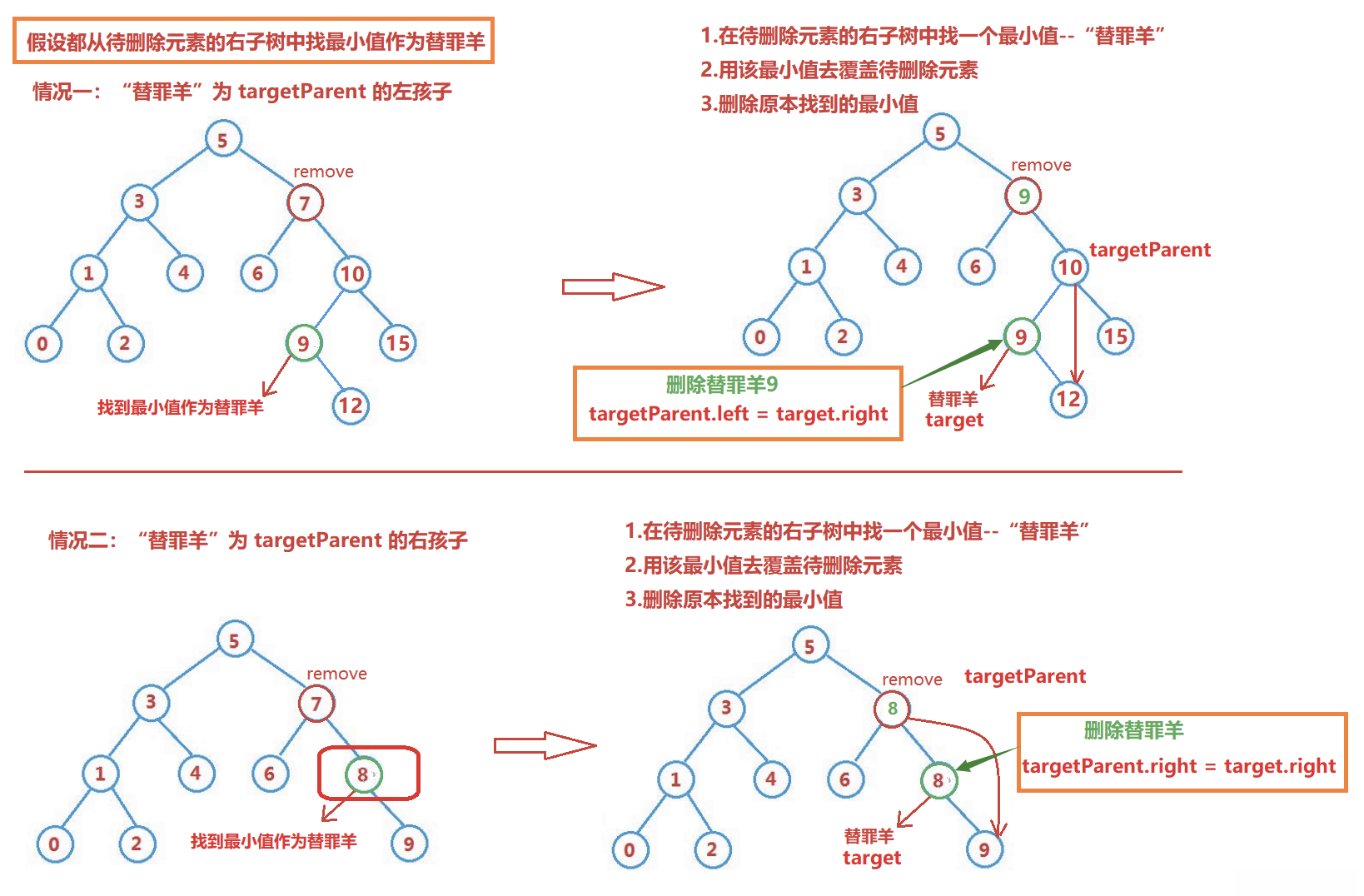
替换法分析

当带删除元素key有左右孩子的时候，直接把key删除是不现实的，因为你根本不知到key下面的结构是什么，就算知道，调整起来也无从下手，所以我们需要借助替换法来实现，既可以选择key的左子树中的最大值进行替换，也可以选择key的右子树中最小值进行替换，因为这样才能保证二叉搜索树的结构不被破坏。

代码如下:

public boolean remove(int key) {
    TreeNode parent = null;
    TreeNode cur = root;
    while (cur != null) {
        if (cur.val < key) {
            parent = cur;
            cur = cur.right;
        } else if (cur.val > key) {
            parent = cur;
            cur = cur.left;
        } else {
            removeNode(parent, cur);
            return true;
        }
    }
    return false;
}
 
private void removeNode(TreeNode parent, TreeNode cur) {
    if (cur.left == null) {
        if (cur == root) {
            root = cur.right;
        } else if (cur == parent.left) {
            parent.left = cur.right;
        } else {
            parent.right = cur.right;
        }
    } else if (cur.right == null) {
        if (cur == root) {
            root = cur.left;
        } else if (cur == parent.left) {
            parent.left = cur.left;
        } else {
            parent.right = cur.left;
        }
    } else {
        TreeNode target = cur.right;
        TreeNode targetParent = cur;
        while (target.left != null) {
            targetParent = target;
            target = target.left;
        }
        // 走到这, target就是要删除节点的右子树中最小的节点, 接下来进行覆盖
        cur.val = target.val;
        // 覆盖完成, 现在需要删除 target 节点
        // 如果 cur.right 没有左孩子的情况, 此时的target就是cur.right
        // 即直接将 cur.right 覆盖到 cur 位置, 也就是满足 target == targetParent.right 条件
        // 所以需要进行特殊处理.
        if (target == targetParent.right) {
            targetParent.right = target.right;
        } else {
            targetParent.left = target.right;
        }
    }
}

2.5 检查插入 / 删除后是否还是一棵二叉搜索树-- 中序遍历

下图中序遍历的结果为：0，1，2，3，4，5，6，7，8，9

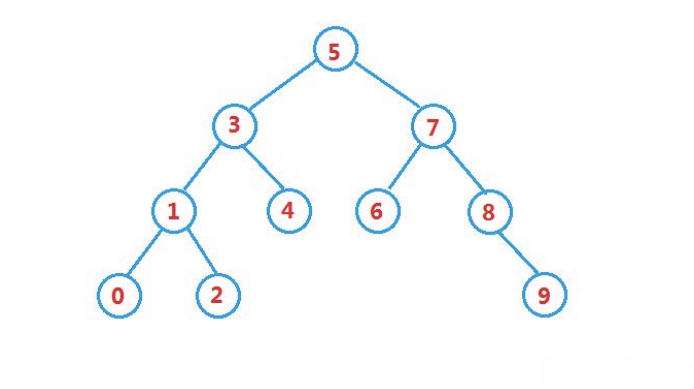
代码如下:

    public List<Integer> inOrder(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        if(root == null) {
            return list;
        }
        List<Integer> left = inOrder(root.left);
        list.addAll(left);//左
        list.add(root.key);//中
        List<Integer> right = inOrder(root.right);
        list.addAll(right);//右
        return list;
    }

咱们在对二叉搜索树进行CURD操作时，就可以通过调用中序遍历的调试和打印来判断是否正确！

---

2.6 性能分析

插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能！

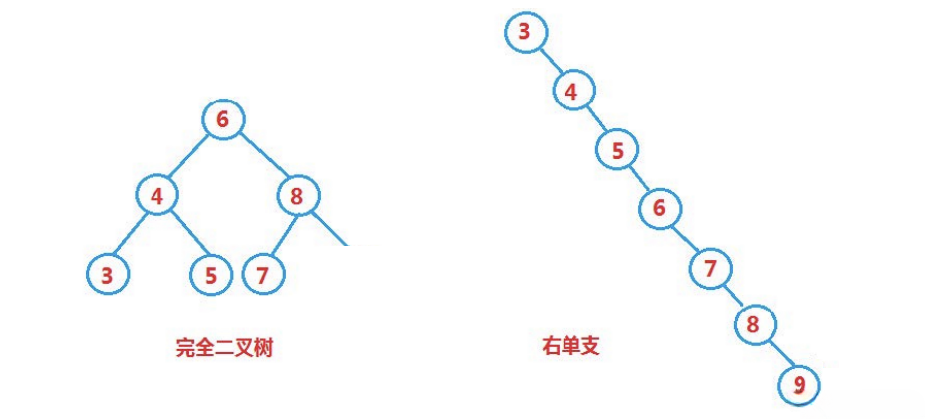
最优情况下，二叉搜索树为完全二叉树，其平均比较次数为：O(log2^N)

最差情况下，二叉搜索树退化为单支树，其平均比较次数为：O(N)